다변수 미적분학 목차 보기
[INTRO] 다변수 미적분학 미리 보기
3차원 벡터 공간 벡터 공간의 정의에 있어 3차원 벡터는 물리적 현상과 같은 현실적 공간을 나타냄에 있어 효과적이다. 그리고 다변수 미적분학은 그러한 3차원 벡터 공간에서의 운동 혹은 물체
hookspedia.tistory.com
INTRO
경로 함수에 대한 미분과 적분의 정의를 알아보고, 그 의미를 해석해보자.
경로 함수의 미분 _ 속도와 가속도
주어진 경로 함수의 미분 정의는 다음과 같다.

경로 함수의 매개 변수 t를 시간으로 두고 함숫값을 위치로 보면, 경로 함수의 미분 결과는 속도가 된다. 그리고 한번 더 미분이 가능하다면, 미분의 결과는 가속도 개념과 일치한다.
그렇다면, 경로 함수의 속도 관점에서 경로 함수가 나타내는 곡선의 길이를 계산할 수 있지 않을까?
근사적 곡선의 길이
주어진 경로 함수 f(t)가 존재한다고 가정하고, 다음과 같이 t의 극한적 정의로 곡선을 나타내 보자.
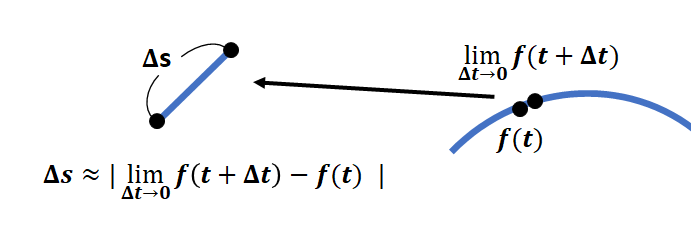
극한적 정의에 따라 곡선의 경로를 직선으로 근사 시킬 수 있다. 그렇다면, 극한적 관점에서 곡선의 미소 길이를 미소 시간으로 나눈 것이 바로 속도일 것이다. 경로 함수에 대한 미분이 속도 개념과 일치하기 때문에 우리는 곡선의 미소 길이를 다음과 같은 적분 형태로 정의할 수 있다.

위와 같은 적분식을 통해서 미소 곡선의 길이(arclength)를 근사하는 함수 S(t)를 구할 수 있다.
전체 곡선의 길이 _ 선 적분
이번에는 곡선의 범위 [a, b]에 해당하는 전체 길이를 구하는 선 적분 개념에 대해 알아보자.
먼저, 함수 S(t)와 매개변수 t의 극한값을 이용하여 경로 함수를 다음과 같은 실함수 F로 매개변수화 한다.

이 새로운 함수 F를 주어진 범위 내에서 적분한다면, 곡선의 전체 경로를 얻게 될 것이다. 이를 선적분이라고 한다.

'MATHEMATICS > Multivariable Calculus' 카테고리의 다른 글
| [Section 1] 경로의 의미 (0) | 2022.04.03 |
|---|---|
| [Section 1] 벡터와 행렬식 (0) | 2022.04.02 |
| [Section 1] 벡터 내적의 의미 (0) | 2022.04.02 |
| [Section 1] 선형 변환 행렬 (0) | 2022.04.02 |
| [Section 1] 벡터 공간과 함수 (0) | 2022.04.01 |



