다변수 미적분학 목차 보기
[INTRO] 다변수 미적분학 미리 보기
3차원 벡터 공간 벡터 공간의 정의에 있어 3차원 벡터는 물리적 현상과 같은 현실적 공간을 나타냄에 있어 효과적이다. 그리고 다변수 미적분학은 그러한 3차원 벡터 공간에서의 운동 혹은 물체
hookspedia.tistory.com
INTRO
벡터에는 단위 벡터를 통해서 그 방향을 나타내고, 스칼라를 통해서 그 크기 속성을 알 수 있다. 기본적인 벡터의 속성을 알아보고, 내적을 통해 어떻게 벡터의 속성이 변화하는지 이해해보자.
벡터의 속성 _ 기준과 크기
벡터에는 기준과 크기 속성이 존재한다. 예를 들어 다음의 2차원 평면을 통해서 두 벡터의 기울기와 길이를 구해보자.
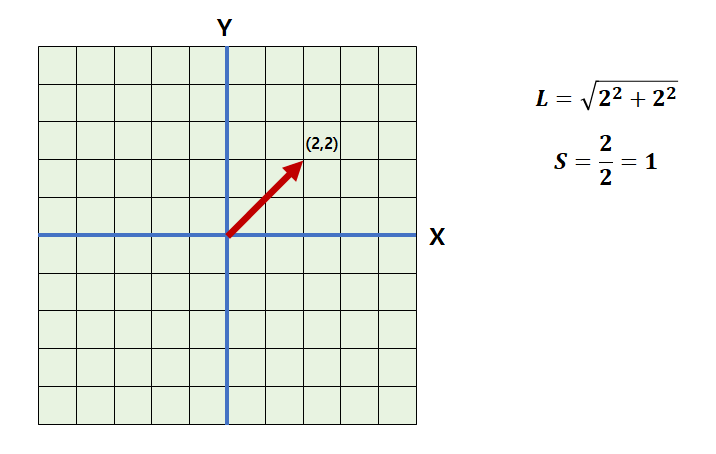
벡터의 길이를 L이라고 할 때, 주어진 벡터의 길이 제곱, L2 = 22+22이다. 그리고 그 기울기는 2/2로 1이 된다. 선형 대수학에서는 벡터의 길이와 기울기 속성을 크기(Magnitude)와 기준(Norm)으로 대신한다. 크기와 기준에 대한 정의는 다음의 정리를 참고하자.

이처럼 벡터의 크기는 자기 자신과의 내적으로 간단히 구할 수 있다. 그렇다면, 만약 두 벡터 A, B가 존재하고 두 벡터의 내적 값이 0이라면 어떻게 될까? 내적 연산은 두 벡터의 관계를 나타내는데도 아주 유용하다.
두 벡터의 관계 _ 거리 속성과 직교 관계
먼저 2차 평면상에서 존재하는 다음의 두 벡터 A와 B를 한번 보자.
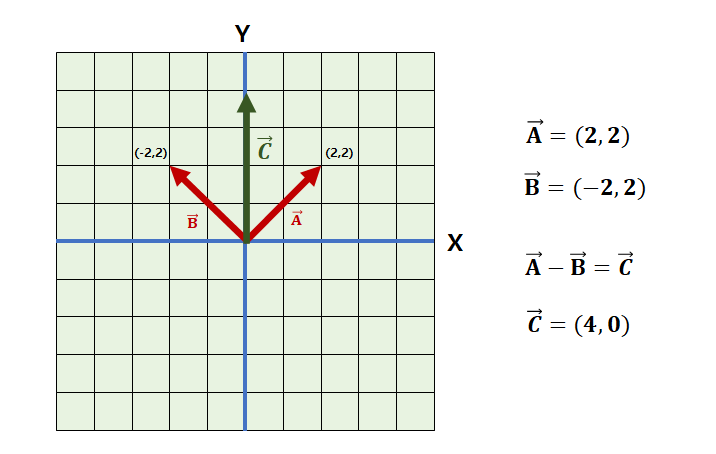
두 벡터의 연산은 새로운 C 벡터를 형성했고, 그 크기는 4이다. 이처럼 두 벡터의 차를 통해 형성된 벡터의 크기가 바로 두 벡터 사이의 떨어진 거리가 된다. 위의 그림에서 새로 형성된 벡터의 크기 속성만을 따져보면, 정확히 A와 B 사이의 거리가 된다. 이 C 벡터는 두 벡터 사이의 거리를 기하학적으로 보여주지 않기 때문에 거리 관점에서 두 벡터의 차이를 새롭게 정의한 개념이 존재한다. 다음의 기하학적 정의를 참고하자.

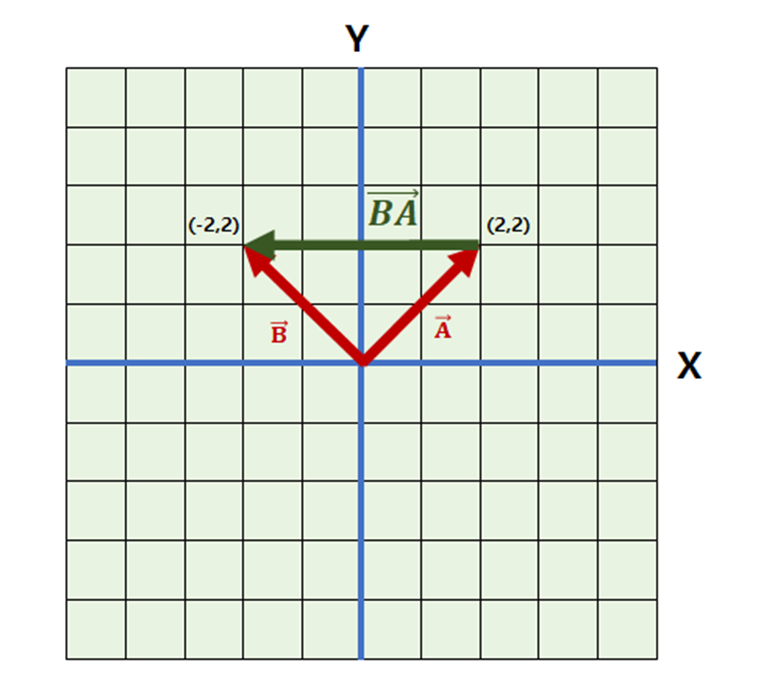
이번에는 두 벡터의 내적 연산을 수행해보자. 두 벡터 A, B의 내적 결과는 0이다. 이것이 무엇을 의미하는가? 두 벡터의 내적 연산은 두 벡터 사이의 각도를 알려준다. 다음의 기하학적 정의를 통해서 내적 연산이 갖는 의미를 이해하자.

결론적으로 두 벡터 A와 B의 내적 결과가 0이라는 것은 두 벡터의 사잇각이 90도라는 사실이다. 즉, 두 벡터의 관계는 서로 수직 하다.
단위 벡터의 등장
벡터의 좌표는 방향을 알려주지만, 크기 속성 때문에 두 벡터의 관계를 복잡하게 만든다. 이에 크기가 1이지만, 그 벡터의 방향을 알려주는 단위 벡터 개념이 등장했다. 단위 벡터의 정의는 다음을 참고하도록 하자.

* 단위 벡터의 정의에 따라, 단위 벡터끼리의 내적은 항상 1보다 작거나 같다.
* 다음 강의는 벡터와 행렬식입니다.
[Section 1] 벡터와 행렬식
다변수 미적분학 목차 보기 [INTRO] 다변수 미적분학 미리 보기 3차원 벡터 공간 벡터 공간의 정의에 있어 3차원 벡터는 물리적 현상과 같은 현실적 공간을 나타냄에 있어 효과적이다. 그리고 다변
hookspedia.tistory.com
'MATHEMATICS > Multivariable Calculus' 카테고리의 다른 글
| [Section 1] 경로 함수의 미분과 적분 (0) | 2022.04.03 |
|---|---|
| [Section 1] 경로의 의미 (0) | 2022.04.03 |
| [Section 1] 벡터와 행렬식 (0) | 2022.04.02 |
| [Section 1] 선형 변환 행렬 (0) | 2022.04.02 |
| [Section 1] 벡터 공간과 함수 (0) | 2022.04.01 |



