* 벡터 분석과 미적분의 기본 목차 보기
[INTRO] 벡터 분석과 미적분의 기본 미리보기
전자기학, 수리물리 등 공학을 위한 벡터 분석방법은 개념 이해와 빠른 지식 응용력을 요구한다. 벡터 분석을 포함하는 기본 미적분 계산은 다양한 분야에 적용되고 있다. 이 목차를 통해서 공
hookspedia.tistory.com
0. INTRO
함수의 연속성을 바탕으로 미분 가능함의 정의와 용어에 대해 자세히 알아본다.
1. 미분 가능(Differentiable)
미분 가능 조건에 대해서 이야기해보자. 먼저, 어떤 집합 X에서 개구간(open interval) (a, b)가 존재한다고 가정한다. 개구간에 포함되는 어떠한 원소 x0에서 미분이 가능할 조건은 다음과 같다.


위에서 정의한 미분 가능 조건의 의미는 함수가 연속해야 한다는 것이다. 이전에 정의한 연속성에 대해서 생각해보면 미분 가능하다는 의미를 충분히 이해할 수 있다.
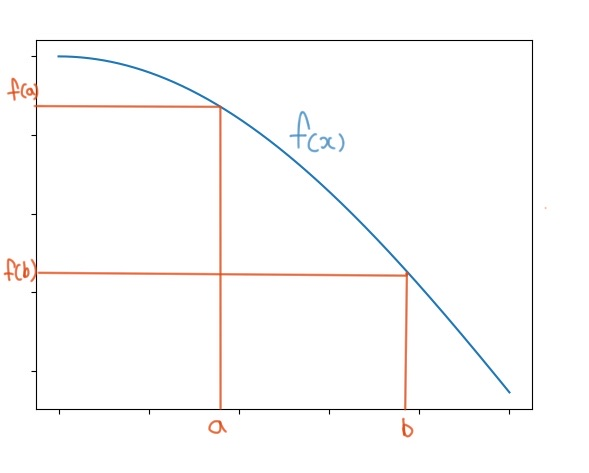
2. 롤의 정리(Rolle's Theorem)
롤의 정리는 미분 개념에서 가장 기본적으로 사용되는 정리 중 하나이다.
가정 조건 : 함수 f(x)가 폐구간 [a, b]에 포함된 임의의 변수 x'를 갖는다고 가정하자.
정리 내용 : f(a)와 f(b)가 같다면, f'(x)가 0이 되는 수가 반드시 하나 이상 존재한다.


이것은 연속된 구간에서 정의가 가능한 미분 개념을 생각해보면 일종의 따름 정리(corollary)라고 생각 할 수 있다.
3. 평균 값 정리(Mean Value Theorem)
이어서 평균값 정리에 대해 알아보자.
가정 조건 : 미분 가능한 함수 f(x)가 존재하고, 임의의 개구간[a, b]에 어떤 변수 x'가 존재한다.
정리 내용 : 다음과 같은 기울기와 동일한 미분 값을 갖는 변수 x'이 반드시 하나 이상 존재한다.
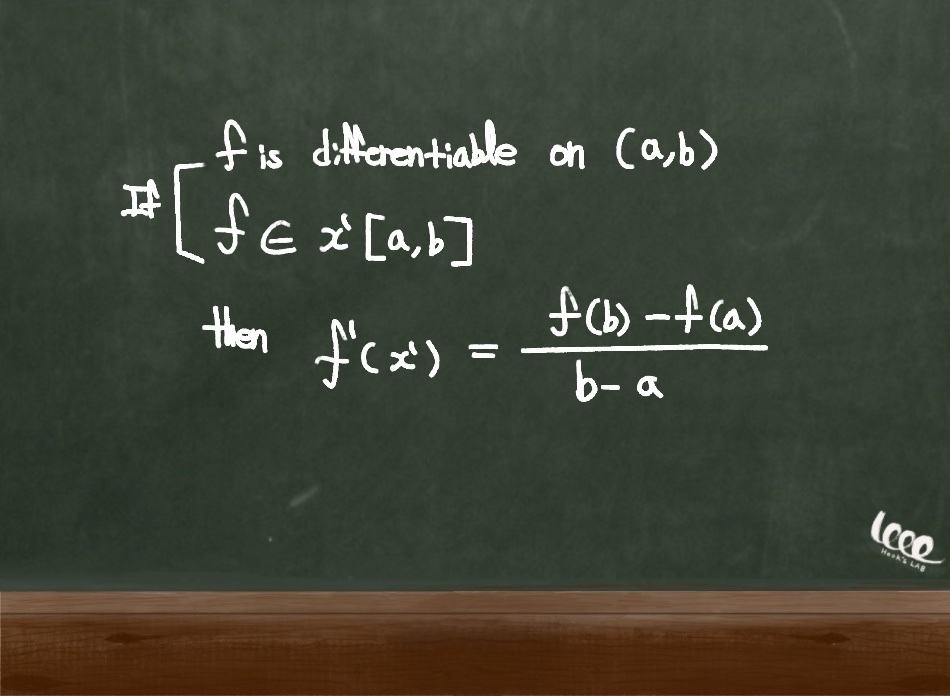

여기서 주목할 만한 점은 개구간(a, b)에 대해서 존재하는 x'이다. a와 b는 같지 않다.
그리고 이것 역시 연속된 구간에서 정의가 가능한 미분 개념과 함수의 기하학적 의미를 고려한다면 일종의 따름 정리이다.
'ENGINEERING > Vector Analysis and Basic Calculus' 카테고리의 다른 글
| [Section 4] 리만적분과 가중평균 정리 (0) | 2021.11.10 |
|---|---|
| [Section 4] 미분조건의 따름 정리들(Corollaries) (0) | 2021.11.09 |
| [Section 4] 함수의 연속성(Continuity) (0) | 2021.11.07 |
| [Section 3] 벡터 필드와 회전(Curl) (0) | 2021.10.13 |
| [Section 3] 벡터 필드와 발산(Divergence) (0) | 2021.10.11 |


