* 벡터 분석과 미적분의 기본 목차 보기
[INTRO] 벡터 분석과 미적분의 기본 미리보기
전자기학, 수리물리 등 공학을 위한 벡터 분석방법은 개념 이해와 빠른 지식 응용력을 요구한다. 벡터 분석을 포함하는 기본 미적분 계산은 다양한 분야에 적용되고 있다. 이 목차를 통해서 공
hookspedia.tistory.com
0. INTRO
미적분학에서 가장 중요한 개념은 아마도 연속성이 아닐까 싶다. 연속성의 정의에 따라서 함수의 성질이 달라지니 말이다. 어떠한 수치를 지정하기 위해서 극한(limit)이라는 용어를 사용하고, 그 연속성을 정의해보도록 하자.
1. 함수의 극한(limit)
어떠한 함수가 다음과 같이 존재한다고 가정하자. 실수 체계에서 이 함수가 연속한다고 어떻게 우리가 정의할 수 있을까?
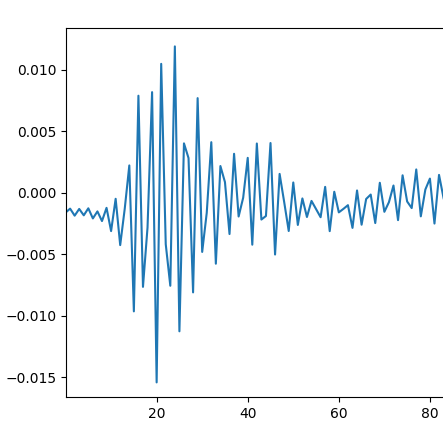
함수의 연속성을 정의하기 위해서 우리는 가장 먼저 함수의 특정 변수를 지정할 수 있어야 한다. 예를 들어 x축의 20을 지정하고 싶다고 하자. 이 20이라는 수를 지정하는 개념이 바로 함수의 극한이다. 기호로는 다음과 같이 표시한다.

이 개념을 사용하여 우리는 어떤 실수 X에서 함수 f(X)가 F값을 가진다는 것을 표현할 수 있다. 즉, f(x)의 변수가 X일 때, 극한값 F를 갖는다. 극한값 개념을 알았으니, 이제 우리는 연속성을 정의할 수 있다.
2. 함수의 연속성(continuity)
실수 체계에서의 연속성을 확립하기 위해 극한값과 그 다음의 연속된 값의 간격인 가장 최소의 단위를 찾아야 한다. 그것은 1인가? 아니다 0.1도 실수이며, 1 보다 더 작다. 그렇다면 0.1이 최소 단위인가? 아니다. 0.01도 실수이며, 더 작다. 그렇다면...
끝없이 반복될 것이다. 우리는 실수 체계에서 불가능해 보이는 연속성을 정의하기 위해서 다음과 같은 최소 단위 개념을 도입했다.
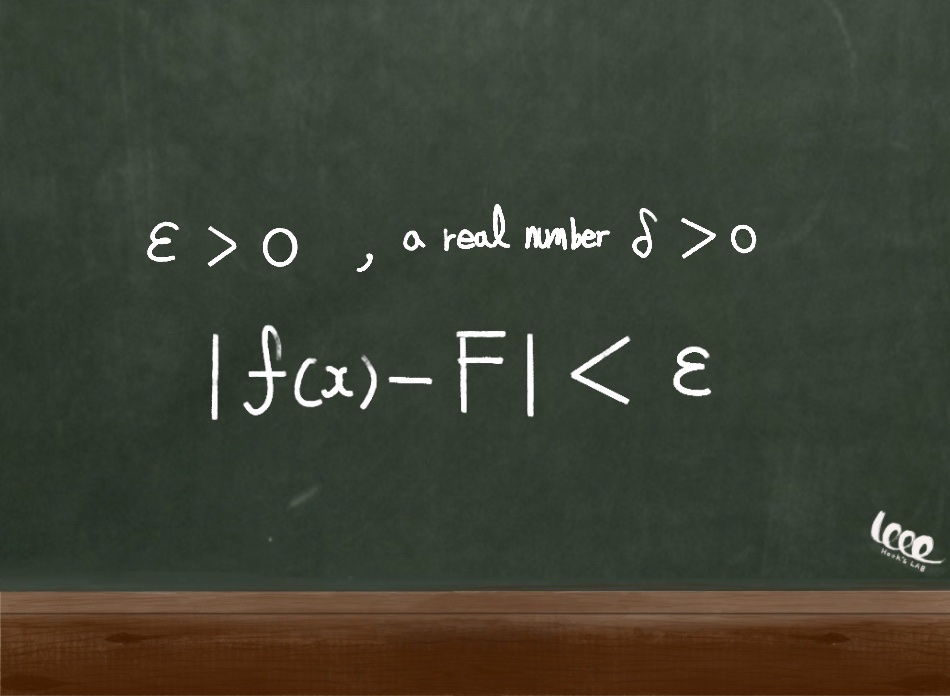
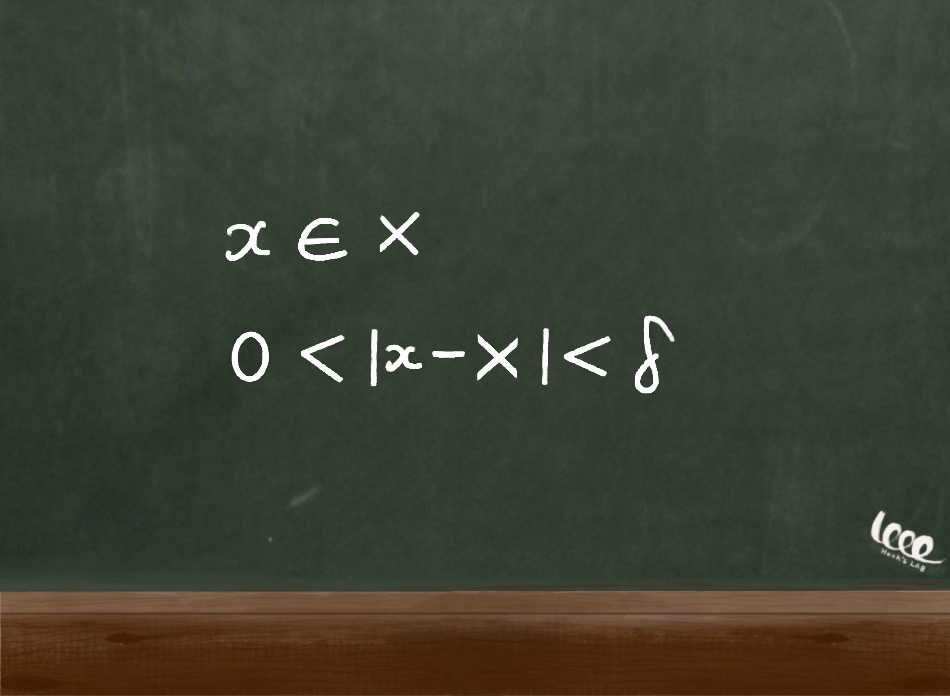
입실론은 0보다 크지만, 극한값에 어떠한 함숫값을 빼더라도 그 최소 단위(입실론)보다는 항상 작은 값이다. 이상해 보이지만 실수 값이고, 이 개념은 실수 체계의 연속성을 정의하기에 부족함이 없다.
일단 연속성의 정의되면 그 구간은 다음과 같이 표시한다.

위와 같이 함수의 연속성이 특정 극한값 구간에서 정의되면, 그 함수는 그 지점에서 연속한다고 말한다. 연속성이 정의된 함수에 대해서 우리는 닫힌 구간(closed interval)을 기호 '['와 ']'으로 다음과 같이 나타낸다. 그리고 그 함수의 수열을 아랫 첨자에 순서 번호를 둠으로써 나타낸다.
* 닫힌구간 [a, b]는 실수 a보다 크거나 같고, b보다는 작거나 같은 실수들의 모임을 말한다.
3. 수렴(convergence)
수렴 개념에서도 연속성과 비슷한 정의가 사용된다. 실수 체계에서는 모든 수에 대해서 연속성을 확립하기 위해서 입실론이 정의되는데, 그 실수의 무한한 순서를 다음과 같이 나타낸다.
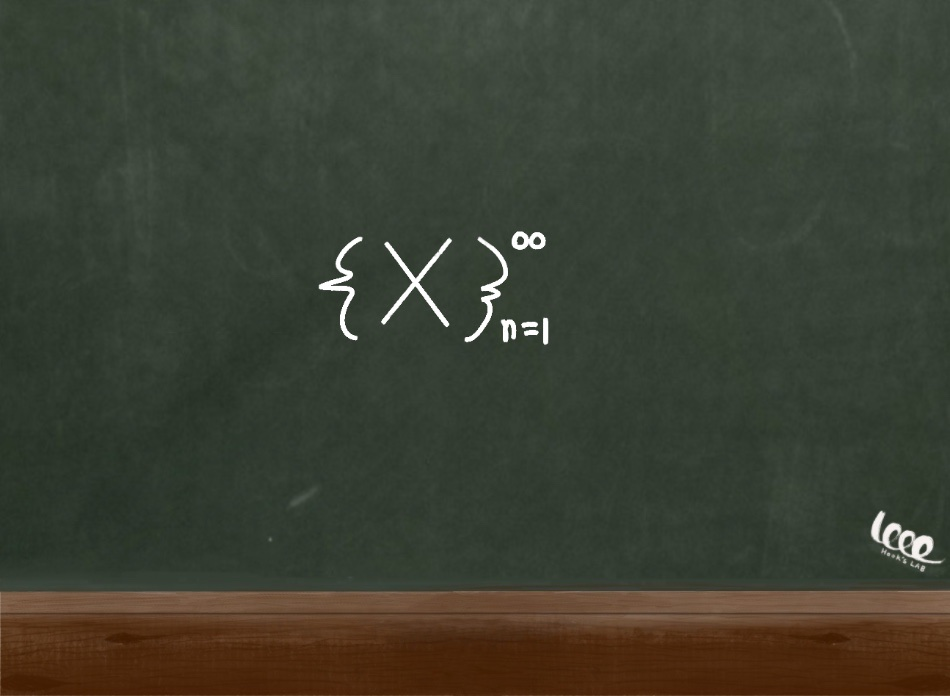
실수인 입실론 중에서 특정한 입실론의 순서에 대응하는 양의 정수 N이 존재한다고 할 때, n이 N보다 크더라도 다음과 같은 조건이 성립한다고 정의한다. 그리고 이를 n이 무한대로 증가함에 따라 함숫값 x_n은 x에 수렴한다고 말한다.
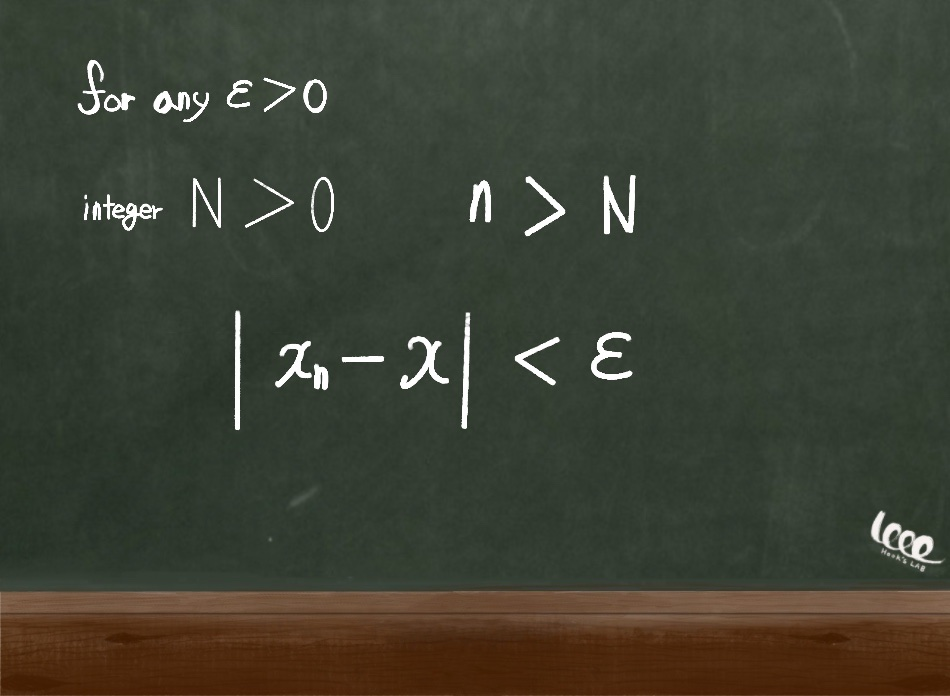
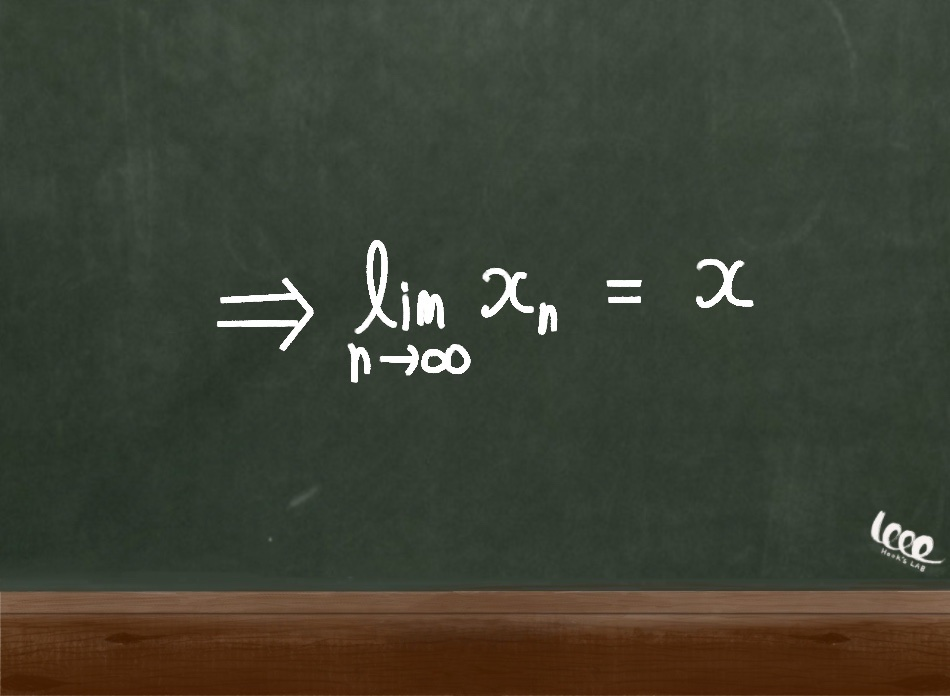
이렇게 연속성과 수렴을 정의함으로써 입실론은 완전무결한 최소 단위 개념을 갖게 되는 것이다.
* 다음 강의는 미분 가능함과 따름 정리입니다.
[Section 4] 미분 가능함과 따름 정리
* 벡터 분석과 미적분의 기본 목차 보기 [INTRO] 벡터 분석과 미적분의 기본 미리보기 전자기학, 수리물리 등 공학을 위한 벡터 분석방법은 개념 이해와 빠른 지식 응용력을 요구한다. 벡터 분석을
hookspedia.tistory.com
'ENGINEERING > Vector Analysis and Basic Calculus' 카테고리의 다른 글
| [Section 4] 미분조건의 따름 정리들(Corollaries) (0) | 2021.11.09 |
|---|---|
| [Section 4] 미분 가능함과 따름 정리(Corollary) (0) | 2021.11.08 |
| [Section 3] 벡터 필드와 회전(Curl) (0) | 2021.10.13 |
| [Section 3] 벡터 필드와 발산(Divergence) (0) | 2021.10.11 |
| [Section 3] 스칼라 함수의 기울기(Gradient) (0) | 2021.10.11 |


