벡터 분석 목차 보기
벡터 분석 미리보기
전자기학, 수리물리 등 공학을 위한 벡터 분석방법은 개념 이해와 빠른 지식 응용력을 요구한다. 이 벡터 분석 공부를 통해서 공학을 위한 벡터 개념을 이해해보도록 하자. Section 1 스칼라와 벡
hookspedia.tistory.com
0. INTRO
스칼라 함수의 기울기를 기술하려면 미분에 대한 개념을 알고 있어야 한다. 스칼라 함수의 기울기를 통해서 3차원 공간에서의 함수 기술에 대해 알아보도록 하자.
1. 그레디언트(Gradient)
스칼라 함수의 그레디언트를 기술하기 전에 다음의 두 스칼라 함수를 보도록 하자.
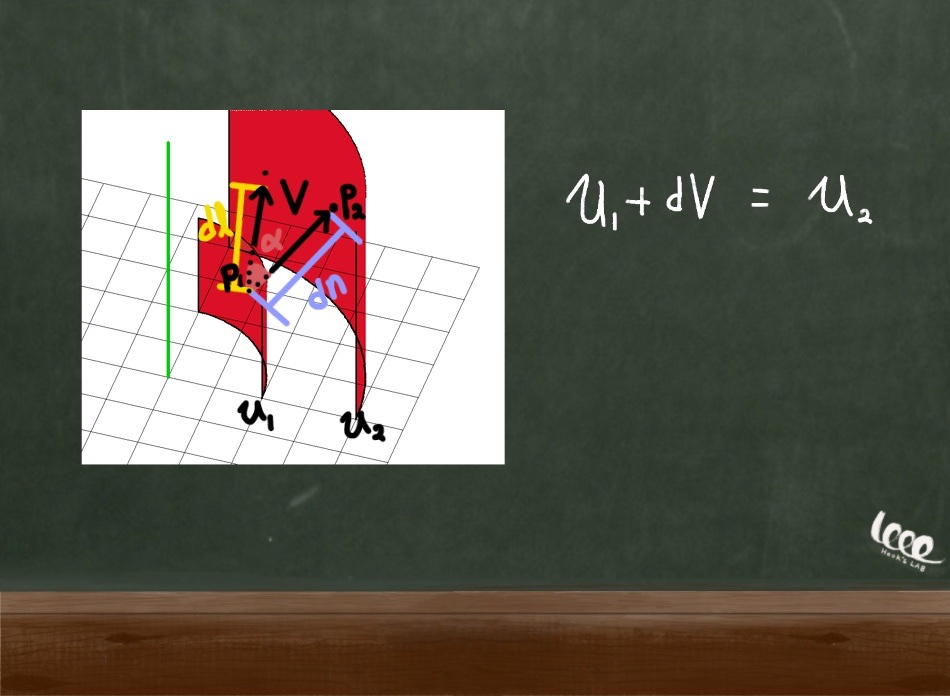
두 스칼라 함수는 대칭적 표면을 가지고 동일하게 발산하고 있다.
두 스칼라 함수의 크기를 각각 u1, u2라고 정의하면, u1에 dV만큼 더한 크기가 바로 u2가 된다.
그렇다면 dV는 무엇을 의미하는가? 여기에서 dV는 u1에서의 미소 변화량을 뜻한다. 일반적으로 dV는 스칼라 함수의 상수 표면 위에 어떤 점을 잡았느냐에 따라서 달라진다.
법전벡터의 길이는 dn으로 표시하였는데, 이 길이가 u1에서 u2로 가는 최단거리가 된다.
이제 그레디언트의 정의를 보도록 하자.

정의에 따라서 그레디언트는 스칼라 함수의 어떤 점에서 나타난 법선 벡터의 크기와 방향을 모두 고려하여 계산한, 스칼라 함수의 최대의 공간 증가율을 의미한다. 보통 Del 기호를 사용하여 나타낸다.
2. 유용한 기울기 개념
기울기 개념은 여러모로 유용한데, 가장 먼저 그레디언트 결과는 벡터를 의미하므로 임의의 스칼라 함수의 공강 증가율을 다음과 같은 계산식으로 구할 수 있다.

다시 말해서, 두 스칼라 함수의 두 상수 평면상에 존재하는 임의의 두 점과 그 사이의 각을 이용하여 공간 증가율을 셈하는 것이 가능하다.
직교 좌표계에서 그레디언트의 기호를 다음과 같이 편미분으로 정의할 수 있다.

* 다음 강의는 벡터 필드와 발산입니다.
[Section 3] 벡터 필드와 발산(Divergence)
벡터 분석 목차 보기 벡터 분석 미리보기 전자기학, 수리물리 등 공학을 위한 벡터 분석방법은 개념 이해와 빠른 지식 응용력을 요구한다. 이 벡터 분석 공부를 통해서 공학을 위한 벡터 개념을
hookspedia.tistory.com
'ENGINEERING > Vector Analysis and Basic Calculus' 카테고리의 다른 글
| [Section 3] 벡터 필드와 회전(Curl) (0) | 2021.10.13 |
|---|---|
| [Section 3] 벡터 필드와 발산(Divergence) (0) | 2021.10.11 |
| [Section 3] 스칼라 함수(Scalar function) (0) | 2021.10.11 |
| [Section 1] 직교 좌표계(Cartesian Coordiantes) (0) | 2021.10.11 |
| [Section 1] 세 가지 종류의 벡터 곱 (0) | 2021.10.09 |



