벡터 분석 목차 보기
벡터 분석 미리보기
전자기학, 수리물리 등 공학을 위한 벡터 분석방법은 개념 이해와 빠른 지식 응용력을 요구한다. 이 벡터 분석 공부를 통해서 공학을 위한 벡터 개념을 이해해보도록 하자. Section 1 스칼라와 벡
hookspedia.tistory.com
0. INTRO
스칼라 함수의 기울기를 구하는 것은 단 하나의 점에 대해서 최대 공간 증가율을 구하는 것과 다름없다. 이러한 함수의 단순화는 복잡한 물리 현상을 기술하는데 적합하지 않다. 이번에는 복잡한 현상을 기술하는데 유용한 발산 개념에 대해 알아보자.
1. 벡터 필드(field)
물리학에서는 여러 가지 종류의 힘을 벡터를 통해서 기술하는데, 3차원에서 작용하는 벡터의 모임을 필드라고 부른다. 이러한 벡터 필드는 장선(flux line)이라는 단순한 선으로써 가시적인 필드를 묘사하는데 그 개념을 사용한다.

일반적으로 방향은 화살표로 나타내며, 그 크기는 단위 부피 혹은 단위 면적을 통과하는 장선들의 수로 정의한다. 스칼라 함수에서 기울기를 통해서 나타낸 크기는 단순한 공간상의 길이였다면, 벡터 필드로 나타내는 그 크기는 어떠한 지점에 작용하는 실질적의 힘의 크기를 묘사한 셈이다.
2. 발산의 정의
어떠한 공간상의 발산을 구하는 것은 그 벡터 필드의 힘의 크기를 구하는 것과 다를 바 없다. 다음과 같이 A필드의 발산을 수식적 정의를 통해서 확인해보자.
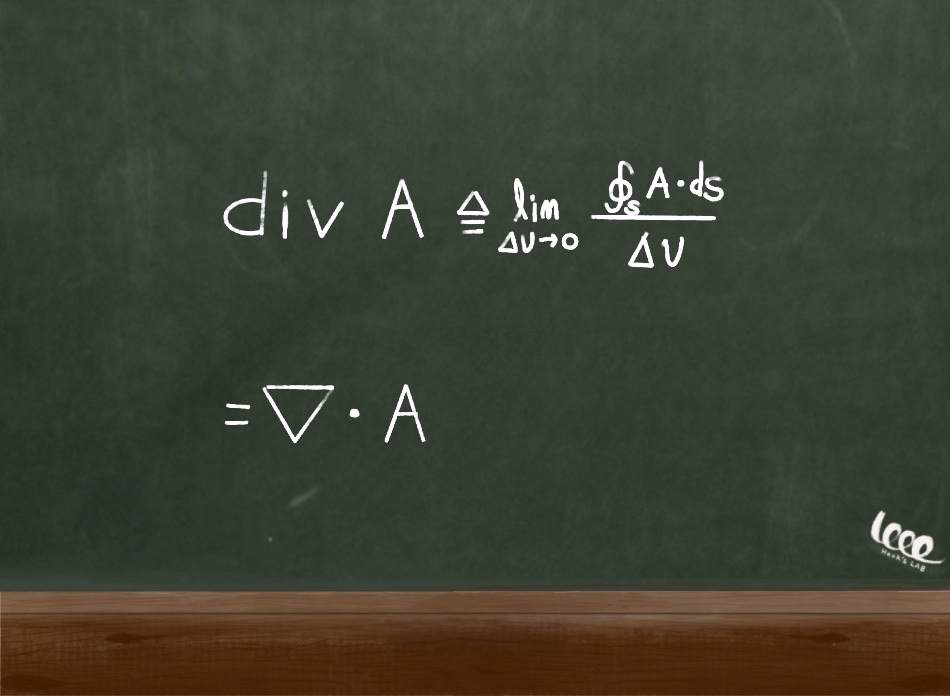
ds에 대해 적분하는 것은 폐곡선에서 어떤 평면 S에 대해서 적분하는 것을 의미한다.
기호는 델과의 내적으로 발산을 표시한다.
3. 발산 정리(Divergence Theorem)
위에서는 폐곡선의 평면에 대해서 적분한 값으로 발산을 정의했다. 이에 가우스는 발산 정리라는 다음의 따름 정리를 도출하였다.
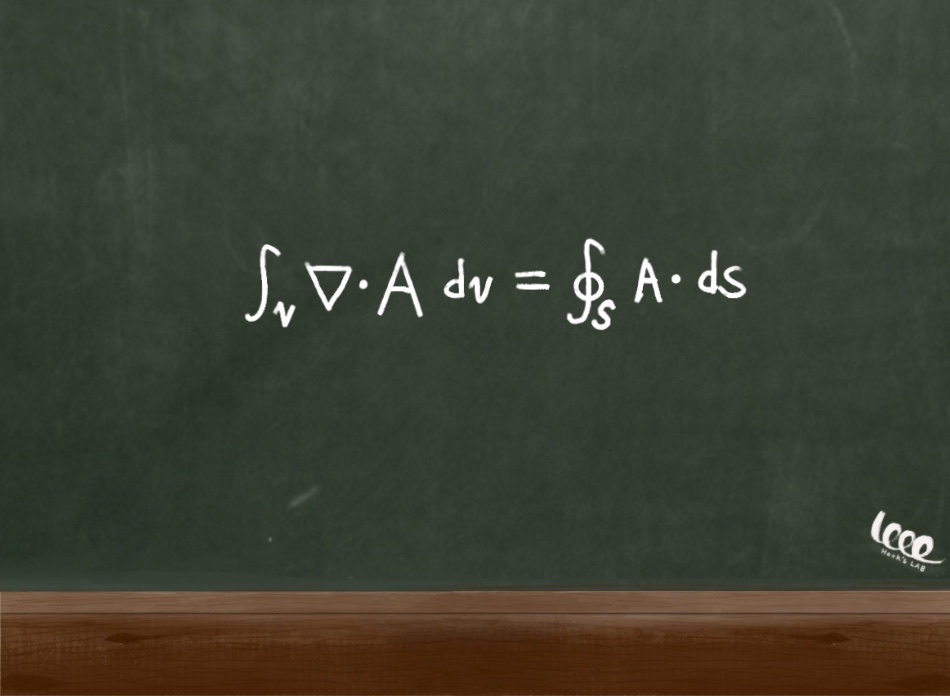
가우스 정리로도 유명한 이 발산정리는 폐곡선 S에 묶인 어느 고리를 포함하는 어떠한 부피에서든 성립한다. 참고로 ds의 방향은 바깥쪽 법선 방향이다.
* 다음 강의는 벡터 필드와 회전입니다.
[Section 3] 벡터 필드와 회전(Curl)
벡터 분석 목차 보기 벡터 분석 미리보기 전자기학, 수리물리 등 공학을 위한 벡터 분석방법은 개념 이해와 빠른 지식 응용력을 요구한다. 이 벡터 분석 공부를 통해서 공학을 위한 벡터 개념을
hookspedia.tistory.com
'ENGINEERING > Vector Analysis and Basic Calculus' 카테고리의 다른 글
| [Section 4] 함수의 연속성(Continuity) (0) | 2021.11.07 |
|---|---|
| [Section 3] 벡터 필드와 회전(Curl) (0) | 2021.10.13 |
| [Section 3] 스칼라 함수의 기울기(Gradient) (0) | 2021.10.11 |
| [Section 3] 스칼라 함수(Scalar function) (0) | 2021.10.11 |
| [Section 1] 직교 좌표계(Cartesian Coordiantes) (0) | 2021.10.11 |



