광학 목차 보기
[Intro] 광학 미리보기
Section 1 2021.04.28 - [PHYSICS/Optics] - [Section 1] 파동 이야기 [Section 1] 파동 이야기 0. INTRO 우리가 살아가는 이 공간은 매질을 통해서 에너지를 전달하고, 그 형태는 파동이다. 물결파, 소리, 심..
hookspedia.tistory.com
INTRO
파동 방정식은 미분방정식으로 파동을 나타낸 것이다. 이를 통해서 미분 방정식의 특성 중 하나인 중첩의 원리(The Superposition Principle)가 그대로 적용된다. 현실에서의 파동 또한 중첩의 원리가 성립하는 것처럼 보인다. 이 중첩의 원리에 대해 자세히 알아보자.
중첩의 원리(The Superposition Principle)
파동 함수의 해(The Solution)가 φ1, φ2 으로 존재한다고 가정하자.
이 두 파동 함수의 해 를 합한 값 역시 파동 함수의 해가 된다.

이렇게 파동 함수는 무한급수처럼, 무수히 많은 수 의 해로 구성되어 있다고 생각해도 된다.
즉, 파동 함수의 해가 무수히 많은 해로 구성되어 있다는 것은 파동 함수가 무수히 많은 파동 함수들의 중첩 상태에 있다는 것을 뜻하며, 이를 다른 파동들이 서로 간섭(Interference) 한다고 표현한다.
파동의 간섭(Interference)
파동의 간섭 현상을 나타내는 두 용어를 알아보기 위해, 두 파동이 존재 한다고 가정하자.
동 위상(In-Phase)
; 위상이 동일하다는 의미로, 두 파동 함수의 위치가 동일하다는 것을 의미한다.
다음과 같이 동 위상에서는 파동의 간섭은 단순한 합으로 중첩된다.

역 위상(Out-of-Phase)
; 역 위상은 두 파동의 위상 차이가 정확히 π 차이가 나는 상태를 의미한다.
다음과 같이 파동의 간섭은 단순한 차이로 중첩된다.
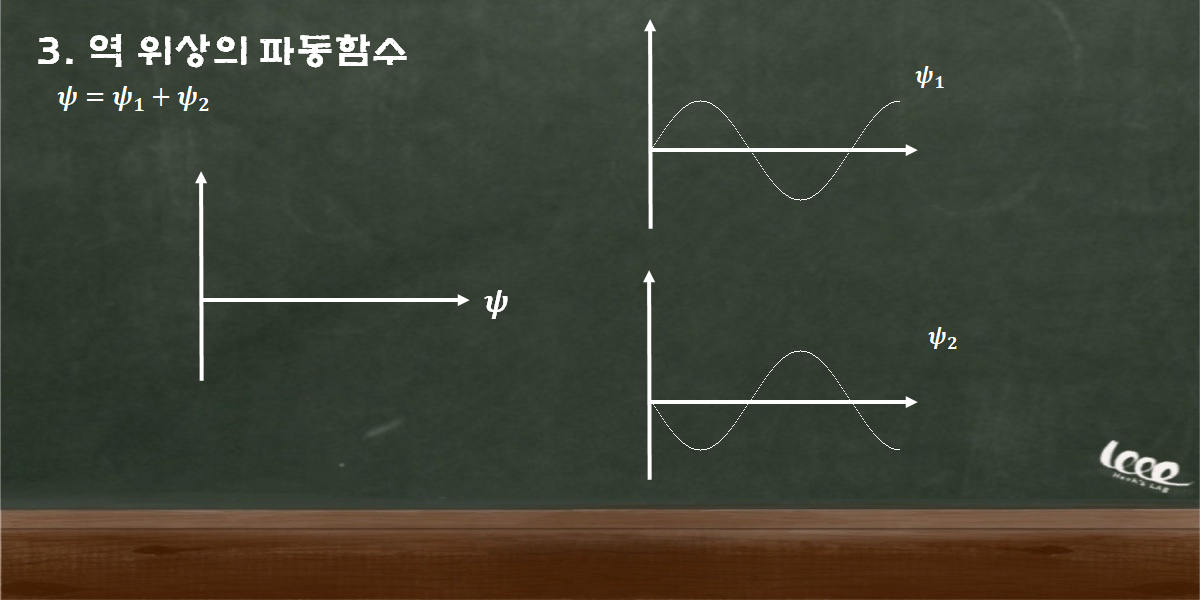
* 그렇다면, 위상의 차이가 π 아니라면 어떻게 중첩된다는 말인가?
동 위상은 더 해주고 역 위상은 빼준다.
이 부분에서 헷갈리기 쉬운데, 그냥 파동의 모든 영역을 합으로 생각하면 편하다.
위상이 π 만큼 차이나면, 음수로 바뀌기 때문이다.
* 다음 강의는 파동의 복소수 표현입니다.
[Section 1] 파동의 복소수 표현
광학 목차 보기 [Intro] 광학 미리보기 Section 1 2021.04.28 - [PHYSICS/Optics] - [Section 1] 파동 이야기 [Section 1] 파동 이야기 0. INTRO 우리가 살아가는 이 공간은 매질을 통해서 에너지를 전달하고,..
hookspedia.tistory.com
'PHYSICS > Optics' 카테고리의 다른 글
| [Section 1] 평면파 (0) | 2021.05.05 |
|---|---|
| [Section 1] 파동의 복소수 표현 (0) | 2021.05.04 |
| [Section 1] 위상과 위상속도 (0) | 2021.05.01 |
| [Section 1] 파동함수의 용어 (0) | 2021.04.29 |
| [Section 1] 일차원 파동 방정식 (0) | 2021.04.28 |



