광학 목차 보기
[Intro] 광학 미리보기
Section 1 2021.04.28 - [PHYSICS/Optics] - [Section 1] 파동 이야기 [Section 1] 파동 이야기 0. INTRO 우리가 살아가는 이 공간은 매질을 통해서 에너지를 전달하고, 그 형태는 파동이다. 물결파, 소리, 심..
hookspedia.tistory.com
INTRO
복소수는 2차원 평면으로 나타낼 수 있다. 가상 영역(Imagnary Part)과 실제 영역(Real Part)이 두 평면의 축이다. 그렇다면 두 축을 이용하여 파동을 기술할 수 있지 않을까? 또, 그렇게 기술한다면 장점은 무엇인가? 파동의 복소수 표현에 대해 알아보자.
복소수와 오일러 공식
복소수 평면에 r 벡터가 있다고 가정하자. 극좌표계로 표현해본다면, x와 y 좌표는 r cos와 r sin으로 나타낼 수 있다. 즉, r 벡터는 가상 영역과 실제 영역의 합 벡터이다. 결과적으로 벡터는 하나의 수학 용어로 기술 가능하다.
그것은 자연로그의 밑인 e이다.
오일러 공식에 따라서 자연로그 e에 관한 함수는 다음과 같이 코사인과 사인 함수의 복소수 형태로 표현 가능하다. x축은 실수(Real) 영역이고, y축은 허수(Imaginary) 영역이 된다.

직교 좌표계에서 r을 1로 볼 때, r 벡터는 간단한 오일러 공식으로 표현이 가능하다.
오일러 공식에 대한 간단하고 유용한 기호를 다음과 같이 정리해두자.

파동의 복소수 표현
복소수 Z는 가상영역과 실제 영역으로 분리가 가능한데, 그 기호는 다음과 같다.

파동을 복소수 형태로 표현하기 위해서는 복소수의 실제 영역만을 취급해야 한다. 그리고 실제 영역을 취급하는 Re 기호는 광학에서 종종 생략하여 나타낸다. 따라서 다음과 같은 수식 표현이 가능해진다.
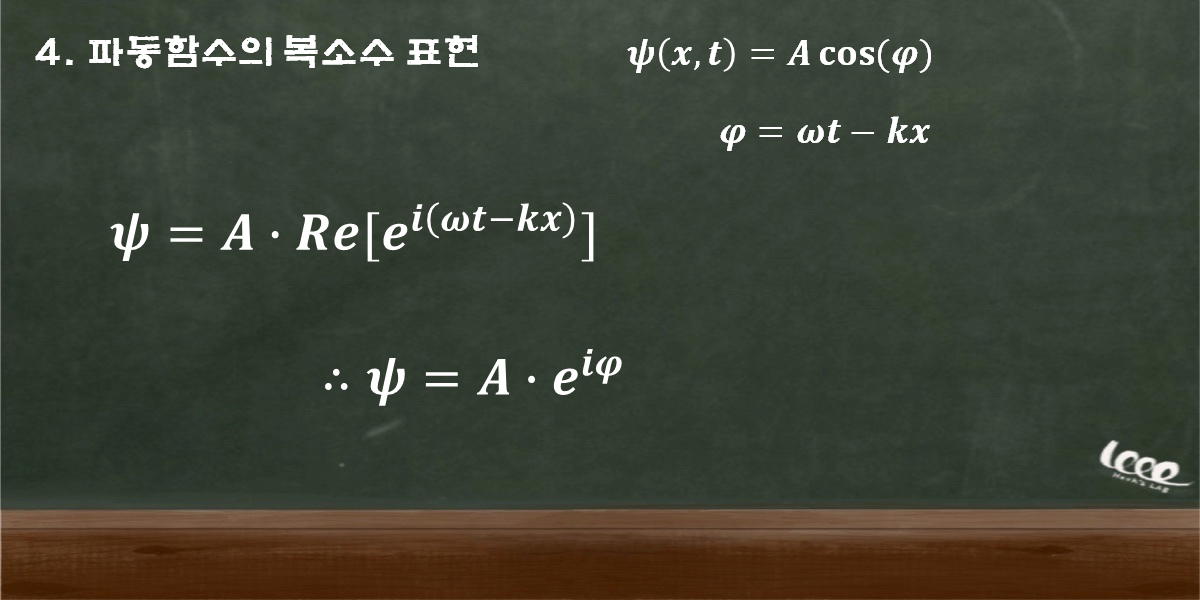
* 다음 강의는 평면파입니다.
[Section 1] 평면파
광학 목차 보기 [Intro] 광학 미리보기 Section 1 2021.04.28 - [PHYSICS/Optics] - [Section 1] 파동 이야기 [Section 1] 파동 이야기 0. INTRO 우리가 살아가는 이 공간은 매질을 통해서 에너지를 전달하고,..
hookspedia.tistory.com
'PHYSICS > Optics' 카테고리의 다른 글
| [Section 2] 레일리 산란 (0) | 2021.05.11 |
|---|---|
| [Section 1] 평면파 (0) | 2021.05.05 |
| [Section 1] 중첩의 원리 (0) | 2021.05.02 |
| [Section 1] 위상과 위상속도 (0) | 2021.05.01 |
| [Section 1] 파동함수의 용어 (0) | 2021.04.29 |



