광학 목차 보기
[Intro] 광학 미리보기
Section 1 2021.04.28 - [PHYSICS/Optics] - [Section 1] 파동 이야기 [Section 1] 파동 이야기 0. INTRO 우리가 살아가는 이 공간은 매질을 통해서 에너지를 전달하고, 그 형태는 파동이다. 물결파, 소리, 심..
hookspedia.tistory.com
INTRO
파동 함수 또한 현상을 이해하기 위해 인간이 만들어낸 언어이다. 파동 함수를 기술하기 위한 용어를 배워보자.
파동 함수와 사인 함수
파동 함수는 삼각함수로 표현이 가능하다. 그 형태와 성질이 유사하기 때문이다.

먼저, 시간 t를 0으로 고정시킬 때 파동 함수는 A sin kx와 같은 형태로 묘사 가능하다.
- 이때, A는 파동의 진폭(Amplitude), k는 파동의 를 나타낸다.
- k는 전파 상수(Propagation number)를 의미한다.
이동하는 파동과 고정된 파동의 차이는 두 번째 식으로 설명이 가능하다. 이것은 파동이 '멈춰있는 상태인가, 아니면 움직이고 있는가'를 알려준다.
파동 함수의 용어
Sin 함수를 바탕으로 파동 함수에 대한 용어를 알아보도록 하자.
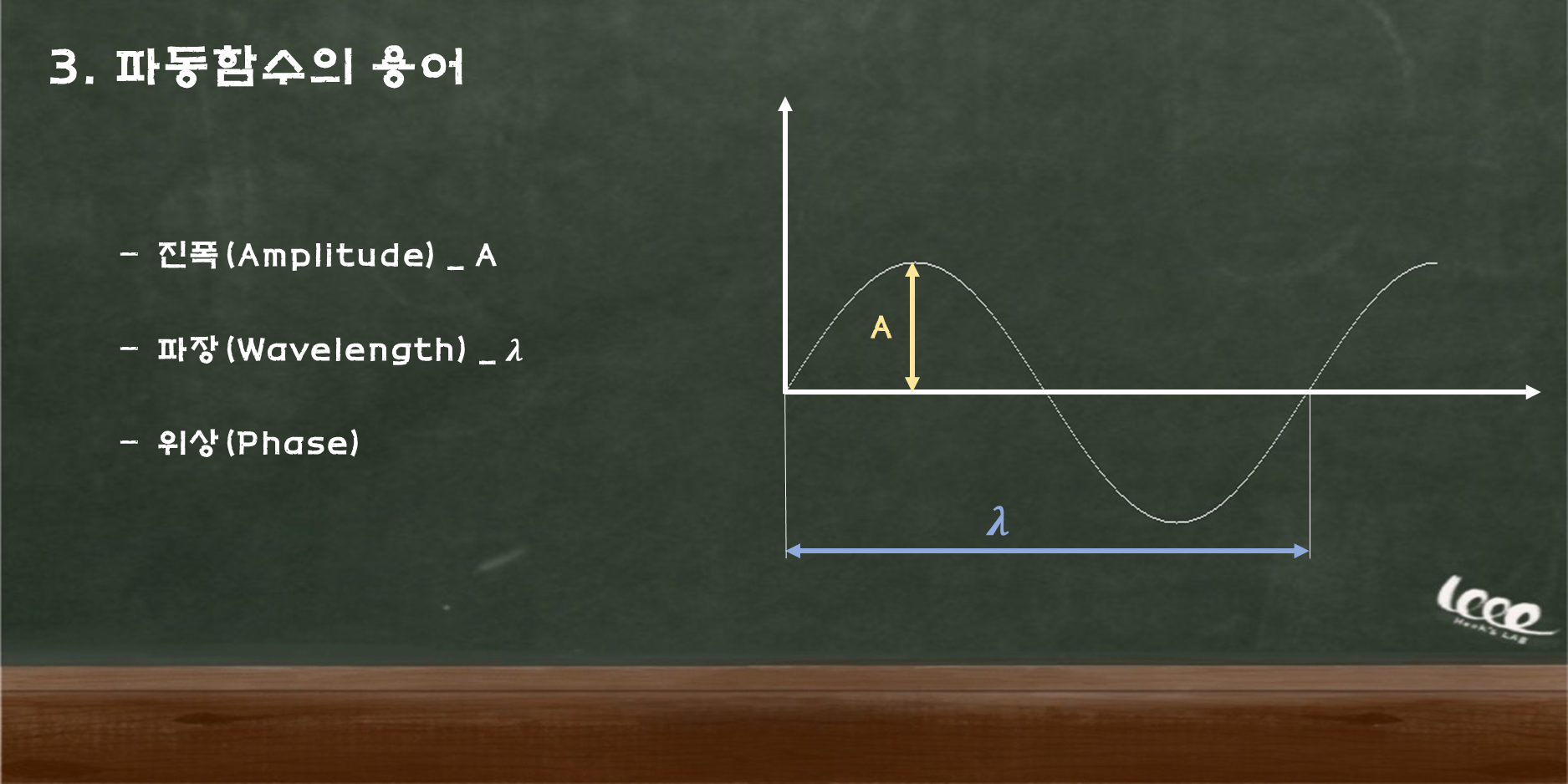
1) 진폭 (Amplitude) ;
사인 함수를 파동 함수로 볼 때, 진폭은 +1과 -1의 절댓값을 나타낸다.
위 그림에서 파동 함수의 진폭은 1이다. (A=1)
2) 파장 (Wave length) ;
사인 함수를 파동 함수로 볼 때, 파장은 사인 함수가 시작점으로 돌아오는 지점까지의 길이를 나타낸다.
이때, 기호는 람다(Lambda)로 표현하다.
3) 위상(Phase) ;
파동 함수의 위치는 위상으로 표현한다.
위상은 파동함수의 위치정보를 나타낸다.
파동 함수 _주기 관련 용어
파동 함수의 가장 중요한 특징 중 하나는 바로 위상이 2 파이 주기로 동일하다는 점이다.

따라서, 위와 같이 파동 함수의 전파 상수, k를 정의할 수 있다. 동일한 방법으로 그 주기를 나타는 시간을 정의할 수 있다. 이때, 타우(Temporal period)는 2파이 위상 동안의 시간을 나타낸다.
다음은 차례대로, 속도와 주파수, 각속도(Angular temporal frequency), 파수(Wave number)를 의미한다.

* 파수는 단위길이당 파동의 수이며, 그 단위는 m의 역수이다.
* 다음 강의는 위상 속도입니다.
[Section 1] 위상과 위상속도
광학 목차 보기 [Intro] 광학 미리보기 Section 1 2021.04.28 - [PHYSICS/Optics] - [Section 1] 파동 이야기 [Section 1] 파동 이야기 0. INTRO 우리가 살아가는 이 공간은 매질을 통해서 에너지를 전달하고,..
hookspedia.tistory.com
'PHYSICS > Optics' 카테고리의 다른 글
| [Section 1] 파동의 복소수 표현 (0) | 2021.05.04 |
|---|---|
| [Section 1] 중첩의 원리 (0) | 2021.05.02 |
| [Section 1] 위상과 위상속도 (0) | 2021.05.01 |
| [Section 1] 일차원 파동 방정식 (0) | 2021.04.28 |
| [Section 1] 파동 이야기 (0) | 2021.04.28 |



