고전 대수학 목차 보기
[INTRO] 고전 대수학 미리 보기
세상의 근본 원리, 본질 등 기본적 물체의 실체를 탐구하는 철학에 있어, 대수학은 항상 그 근원적인 문제에 대한 질문을 야기한다. 하나의 진실된 명제가 있다면, 그것은 무엇인가? 대수학의 특
hookspedia.tistory.com
0. INTRO
집합이라는 하나의 수학 체계를 구성함으로써, 논리적 증명과 고찰이 더 수월하여진다. 자연수는 수를 세거나, 순서를 매길 때 사용되는 수 체계로, 음이 아닌 정수와 양의 정수의 집합으로 구성된다. 이 집합은 페아노 공리계(Peano’s axioms)라고 불리는 자연수 체계를 묘사하는 공리들로 정의된다.
1. 술어 논리(predicate logic)
A. 종속 변수( Bound variable)
다음의 명제를 보자.
"모든 정수는 자연수이다. "
or
"All integers are natural numbers."
위의 명제처럼, 1가 술어(one-place predicates)로 이루어진 위 명제는 z라는 글자를 이용하여, 같은 뜻을 가진 명제가 다음과 같은 형태로 다시 쓰일 수 있다.
"모든 z에 대해서; 만약 z가 정수이면, z는 자연수이다."
or
"For all z; If z is an integer, then z is a natural number"
이 명제에서 z라는 변수는 하나의 숫자로 결정될 수 없다. 앞의 "모든"이라는 연산자가 z 변수를 하나의 특성을 가지는 변수로 종속시켰기 때문이다. 이러한 변수를 종속 변수(Bound variable)라고 한다.
B. 자유 변수(Free variable)
다음의 명제를 보자.
"정수 z는 자연수이다."
이 명제에서는 z는 정수라는 집합의 어떤 수 도 될 수 있기 때문에, 자유 변수(free variable)라고 부른다.
C. 보편 양화사(Universal quantification)
"모든"과 같은 연산자(operator)를 보편 양화사(universal quantification)이라고 부른다. 이 보편 양화 사는 논의 영역에 속하는 모든 원소가 주어진 명제를 만족시킬 수 있다는 것을 의미하는 말이다.
D. 존재 양화사(Existential quantifier)
존재 양화사는 명제에서 술어에 해당하는 객체가 적어도 하나 이상 존재함을 의미하는 연산자이다. 일반적인 언어로 표현하면 "~가 존재한다(There exist ~)", 혹은 "어떠한 x에 대해서든(For some x:): x는 ~이다."
2. 수리 논리의 기호
A. 보편양화사와 존재 양화사
임의의 명제적 형태인 H가 존재한다고 할 때, 대부분의 수학 문헌에서 사용된 보편 양화사의 기호는 다음과 같다.

마찬가지로 존재 양화사의 수학적 기호는 다음과 같다.

B. 항등식 기호(notation)
항등식 기호로 등호 표시인 '='는 일상에서도 쉽게 마주할 수 있다.
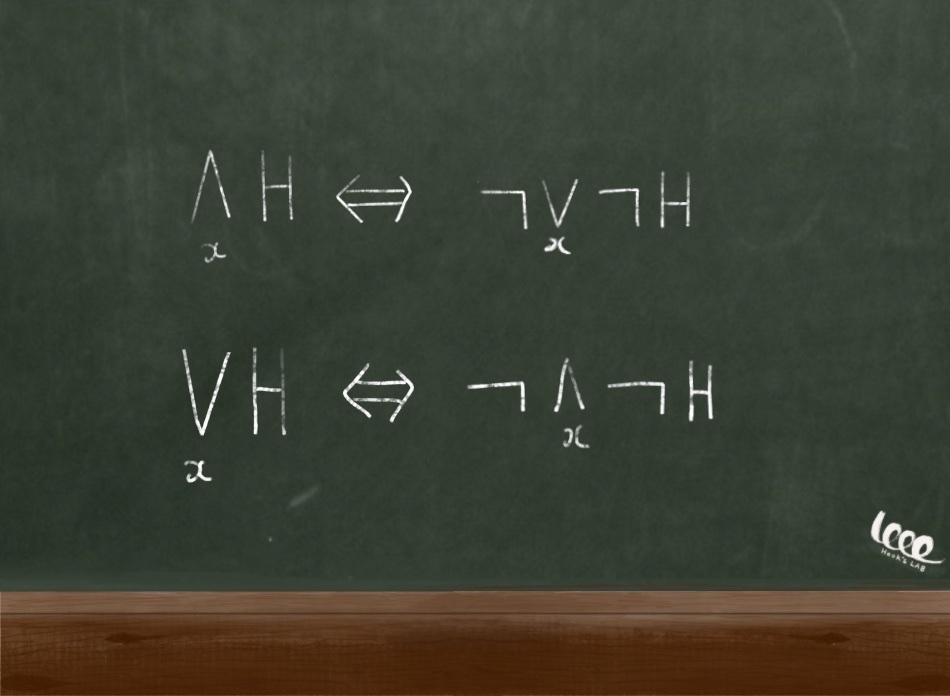
C. 설명 연산자(description operator)
H 명제가 "~는 자연수이다" 일 때, 다음의 기호를 살펴보자.
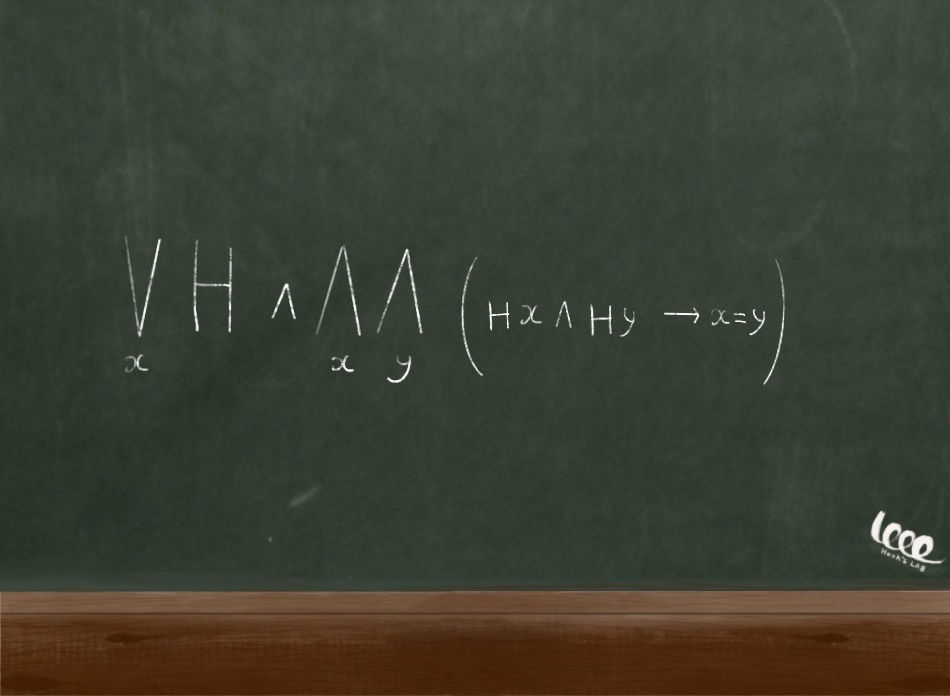
명제를 나타내는 기호의 정의에 의해 위 명제는 "모든 x가 자연수이고, x와 y가 존재한다 (x가 자연수이고 y도 자연수이면 x와 y는 같은)"라는 뜻을 가진다. 이때 괄호()를 설명 연산자라고 한다.
* 다음 강의는 논리적 귀결에 대해서입니다.
[Section 1] 논리적 귀결에 대해서...
대수학 목차 보기 [INTRO] 대수학 미리보기 세상의 근본 원리, 본질 등 기본적 물체의 실체를 탐구하는 철학에 있어, 대수학은 항상 그 근원적인 문제에 대한 질문을 야기한다. 하나의 진실된 명제
hookspedia.tistory.com
'MATHEMATICS > Classical Algebra' 카테고리의 다른 글
| [Section 1] 알고리즘과 논리학 증명 시스템 (0) | 2021.07.23 |
|---|---|
| [Section 1] 공리계의 성질 (0) | 2021.07.21 |
| [Section 1] 논리적 귀결에 대해서... (0) | 2021.07.19 |
| [Section 1] 명제의 논리적 기능 (0) | 2021.07.19 |
| [APPENDIX] 방정식의 기본 (0) | 2021.07.15 |

