일반 대수학 목차 보기
[INTRO] 일반 대수학 미리보기
언어의 모순성 플라톤은 이데아라는 개념을 통해서 모든 인식 객체의 초월적 실체를 주장했다. 모든 실체는 반드시 초월적 실체를 가져야 할까? 한편, 고대 로마 시기의 그리스
hookspedia.tistory.com
INTRO
집합의 개념이 어느 정도 잡혔으니, 이제 집합 개념을 조금씩 확장해보자. 먼저, 집합에는 정수, 유리수와 무리수, 그리고 실수까지 집합의 확장이 가능하다. 그리고 이들의 관계는 벤 다이어 그램으로 나타내는 것이 널리 알려져 있다. 이들의 관계를 기호로 간략히 나타내어보자.
자연수부터 정수, 유리수, 그리고 실수까지
자연수(Natural numbers)는 일반적으로 0을 제외하는 양의 정수로 흔히 표현한다. 이 자연수는 보통 수를 셀 때 사용되는 개념이기에 0을 원소로 갖지 않는다. 그리고 정수(Integers)는 양의 정수, 음의 정수로 보통 다시 나눌 수 있다. 이 정수 집합은 0을 원소로 포함하는 것이 가장 큰 특징이다. 또 유리수(Rational numbers)는 정수의 비율로 분모가 0이 되는 경우를 제외한 수를 원소로 갖는다. 한편, 유리수로 모든 소수를 표현할 수 없다는 특징을 가지고 있다. 그로 인하여 무리수(Irrational numbers)라는 개념이 존재하는데, 이 무리수는 두 정수의 비로 나타낼 수 없는 실수(Real numbers)이다. 즉, 실수는 지금까지 열거한 집합들을 모두 하위 집합으로 갖는 집합이 된다. 수 집합에 대한 수학적 정의는 다음을 참고하자.

수 집합의 크기는 어떻게 정의할까? 대수학에서는 모든 수 집합은 무한한 원소를 가질 수 있음에도, 유한한 집합의 크기로 정의한다. 이는 모든 집합의 원소가 일대일 대응 관계가 성립함을 보일 수 있기 때문이다. 다시 말해서, 지금까지 정리한 모든 집합들은 셀 수 있는 집합들이며, 간단히 자연수 집합의 크기인 알레프 제로(aleph zero)의 형태로 나타낸다. 그렇다고 해서 모든 집합의 크기가 같다는 말은 아니다. 집합의 크기는 순서 관점의 비교이다. 이는 다음 강의에서 다루기로 하자.
집합의 관계 _ 합집합과 교집합
다음은 위에서 정리한 집합들을 벤다이어그램으로 간단히 나타낸 그림이다.
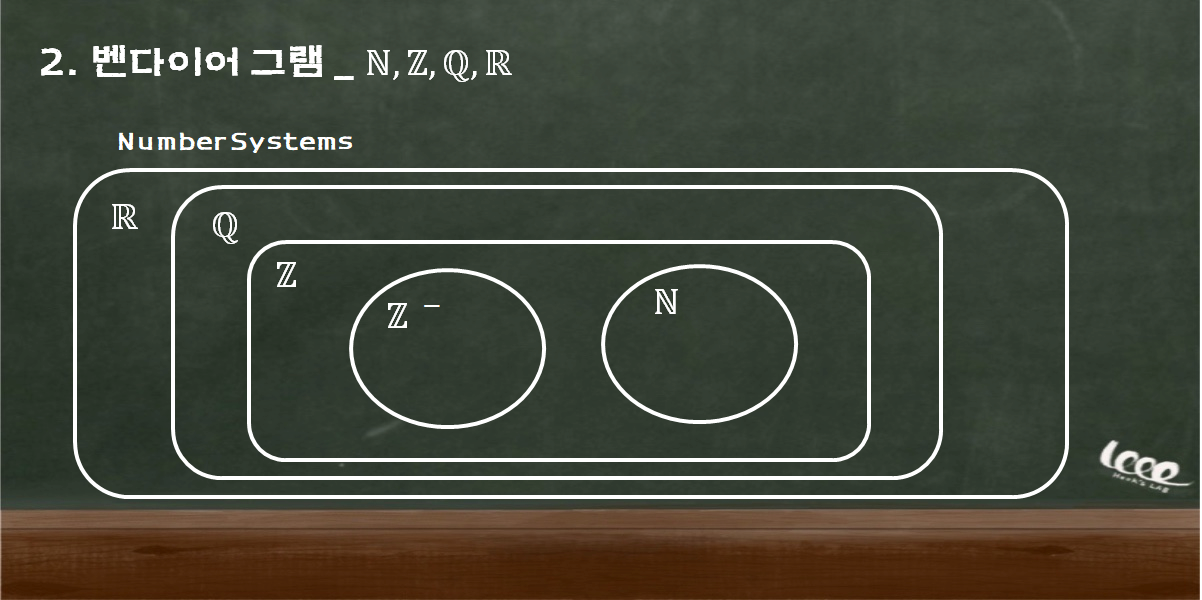
그림으로 쉽게 그 관계를 알 수 있지만, 이를 표현하는 수학적 기호는 따로 있다. 다음을 참고하자.

집합의 크기 비교
집합의 크기 비교는 일반적으로 기호 <, >, = 등을 사용하여 나타낸다. 집합의 크기 비교에 관하여 유용한 정리인 칸토어-번슈타인 정리를 다음과 같이 정리해두겠다.

집합의 크기를 비교하는 과정에서 나타난 부분 순서(Paritial order)와 기수(Cardinal) 개념은 집합의 비교에 있어서 중요하다. 따라서 다음 강의는 이 개념들에 대해서 자세히 다루도록 하겠다.
* 다음 강의는 부분 순서 집합의 의미입니다.
[Section 1] 부분 순서 집합의 의미
일반 대수학 목차 보기 [INTRO] 일반 대수학 미리보기 언어의 모순성 플라톤은 이데아라는 개념을 통해서 모든 인식 객체의 초월적 실체를 주장했다. 모든 실체는 반드시 초월적 실체를
hookspedia.tistory.com
'MATHEMATICS > Algebra' 카테고리의 다른 글
| [Section 2] 수학적 귀납법의 원리 (0) | 2022.03.25 |
|---|---|
| [Section 1] 부분 순서 집합의 의미 (0) | 2022.03.24 |
| [Section 1] 집합의 분할 (0) | 2022.03.20 |
| [Section 1] 등가 관계와 동치 관계 (0) | 2022.03.04 |
| [Section 1] 함수의 종류 (0) | 2022.03.01 |



