[Section 3] 자기장의 경계조건(Boundary Condition)

전자기공학 목차보기

[INTRO] 전자기공학 미리보기

0. INTRO

주어진 영역에 대한 자기장 문제를 해결하기 위해서, 경계조건에 대한 이해는 중요하다. 이는 경계면에서 다른 물질이 존재할 때, 경계조건을 통해서 물질의 영역을 구분할 수 있기 때문이다. 전기장에서의 경계조건과 유사한 방식으로 자기장 경계조건을 기술해 보도록 하자.

1. 경계면과 수직 한 자기장

물질 A와 B가 맞닿아 있고, 그 경계면에서의 자기장을 상상해보자.

 

수직한 성분의 자기장

 

자기장의 원천은 전류의 회전에 의한 것이다. 전기장의 경우 수직 한 방향은 그 발산의 원천인 전하만큼 불연속적이었지만, 자기장은 발산하지 않기에 수직 한 성분은 연속적으로 다음과 같이 기술된다.

 

연속한 자기장

2.  선형, 등방성 물질의 자기장

물질이 선형이고 등방성이라고 가정하면, 다음과 같은 관계가 성립한다.

 

등방성 물질

 

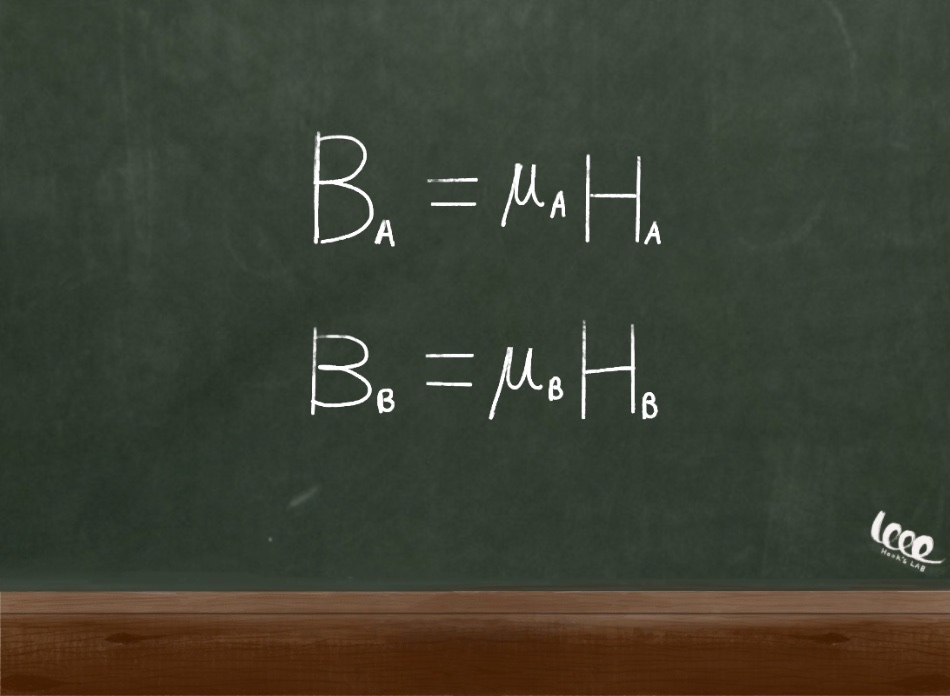
즉, 경계면에서의 대체 전기장 또한 다음과 같이 연속적이다.

 

수직한 자기장의 연속성

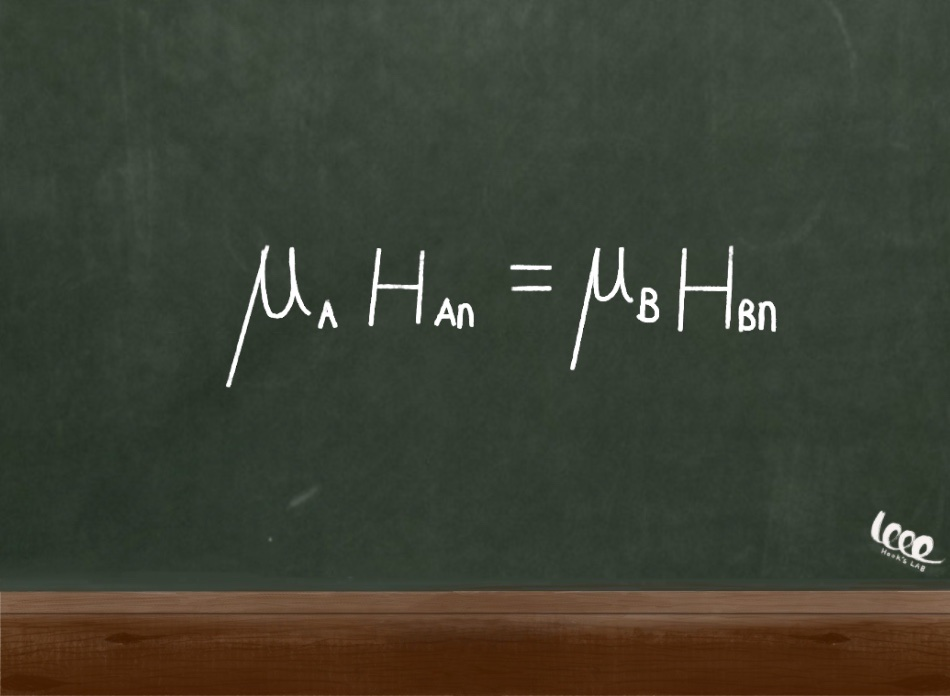
3.  경계면과 접선 방향의 자기장

전기장에서와 다르게 경계면과 접하는 방향의 자기장은 불연속적이다. 이는 경계면에서 자기장을 따라 선 적분한 값이 바로 전류밀도에 해당하기 때문이다. 

 

불연속적인 접선 방향 자기장

 

하지만, 이 경우는 표면 전류가 경계면을 따라서 존재하는 경우에만 성립한다. 일반적으로 전도성이 유한한 물질들의 경우, 절류들은 부피 전류 밀도로 구분하고 이때는 표면 전류는 존재하지 않는다고 가정한다. 따라서 접선 성분 또한 연속적이라고 볼 수 있다.

 

연속적인 접선 방향 자기장

 

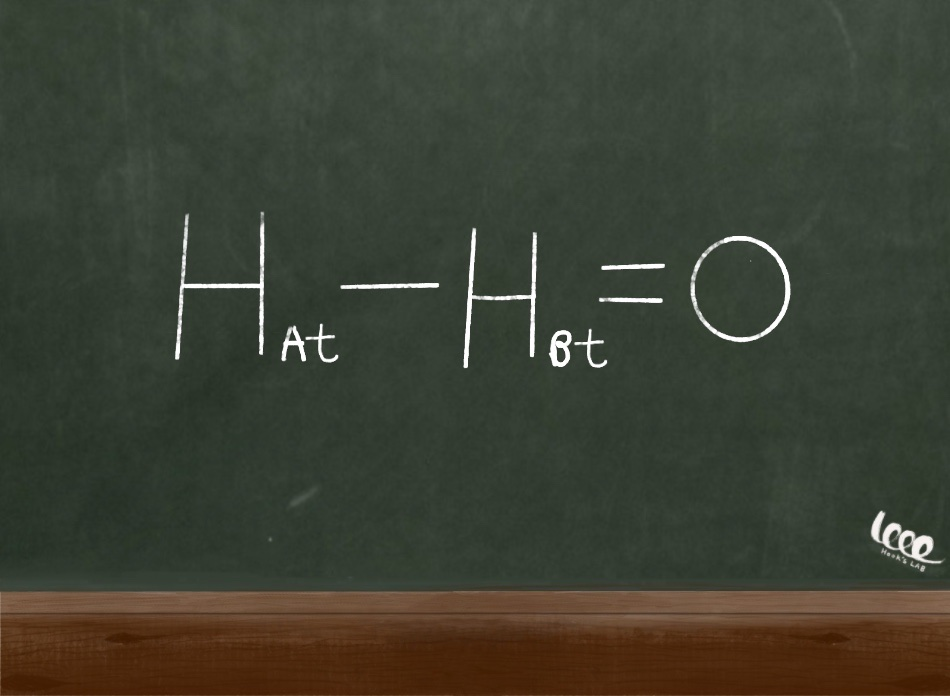
* 초전도체나 이상적으로 완벽한 전도 물질은 표면 전류밀도가 존재한다!

 

* 다음 강의는 인덕터의 자기장입니다.