자료구조와 알고리즘 목차 보기
[INTRO] 자료구조와 알고리즘
자료구조와 알고리즘에 대해서... 자료구조는 프로그래밍에서 사용되는 데이터를 어떻게 표현하는 것인가에 대한 컴퓨터 과학 분야이다. 그리고 알고리즘은 표현된 데이터를 계산하는 방법에
hookspedia.tistory.com
0. INTRO
이진트리의 순회 알고리즘과 유사하게 그래프에도 꼭짓점 노드에 대한 탐색 알고리즘이 존재한다. 가장 먼저 알아볼 탐색 알고리즘은 깊이 우선 탐색(Depth First Search) 알고리즘이다. 이는 코딩 테스트의 주요 기출문제로 자주 나오기도 한다.
1. 깊이 우선 탐색 기법의 이해 _ 모든 꼭짓점 노드를 방문하는 방법
깊이 우선 탐색기법을 위해 다음의 예시 그래프를 참고하도록 하자.

예시 그래프에서 보이는 바와 같이 A에서 I로 도착하는 경로는 몇 가지나 될까? 만약 E에 도달하면 목적지에는 결코 도달할 수 없을 것이다. 따라서 이 물음에 답하기 위해서는 모든 경로를 고려해야 하기 때문에 모든 꼭짓점 노드에 접근하는 것이 핵심이다.
깊이 우선 탐색, DFS는 백트래킹 알고리즘을 이용하여 구현된다. 구현될 백트래킹 알고리즘의 꼭짓점 노드 방문 순서와 과정을 다음의 과정을 참고하여 알아보자.


혹시 위 과정을 보고 DFS 알고리즘이 무엇인지 감이 오는가?
오지 않는다면, 계속해서 과정을 지켜보도록 하자.

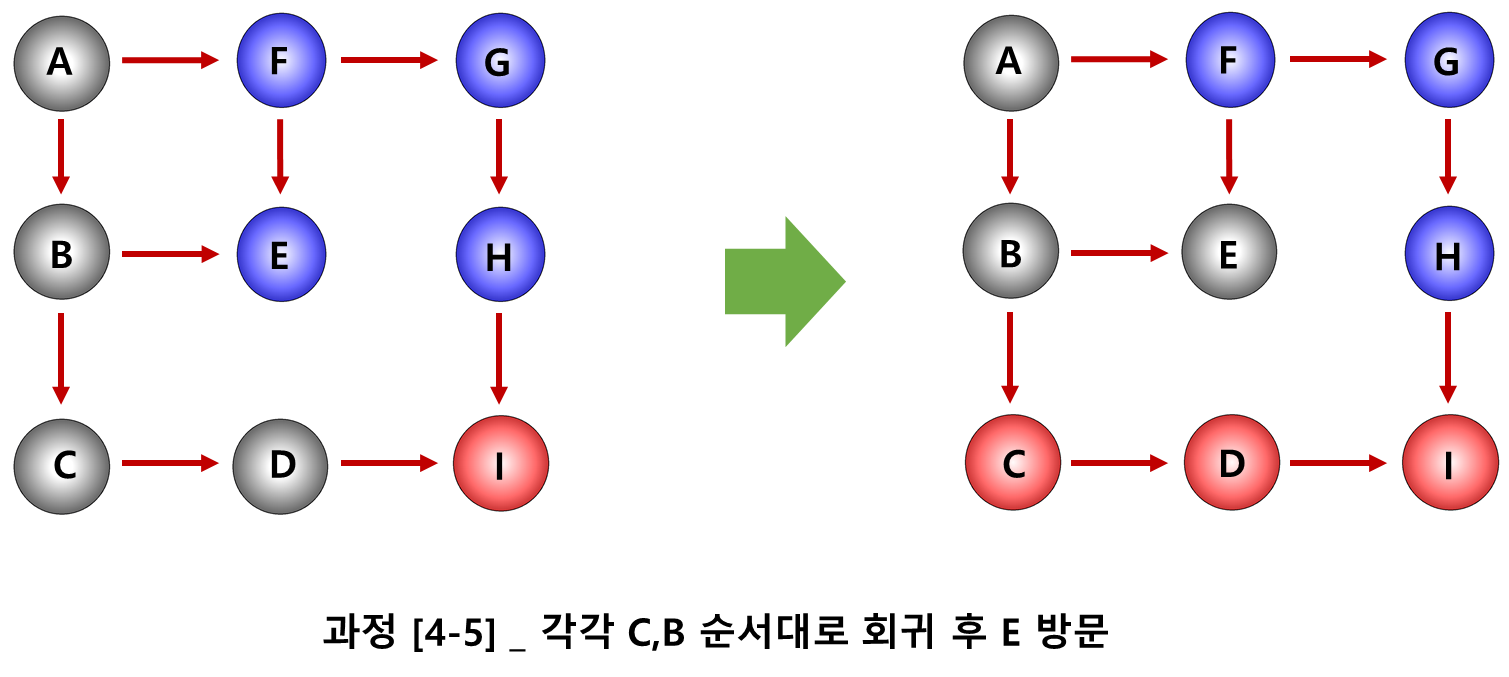
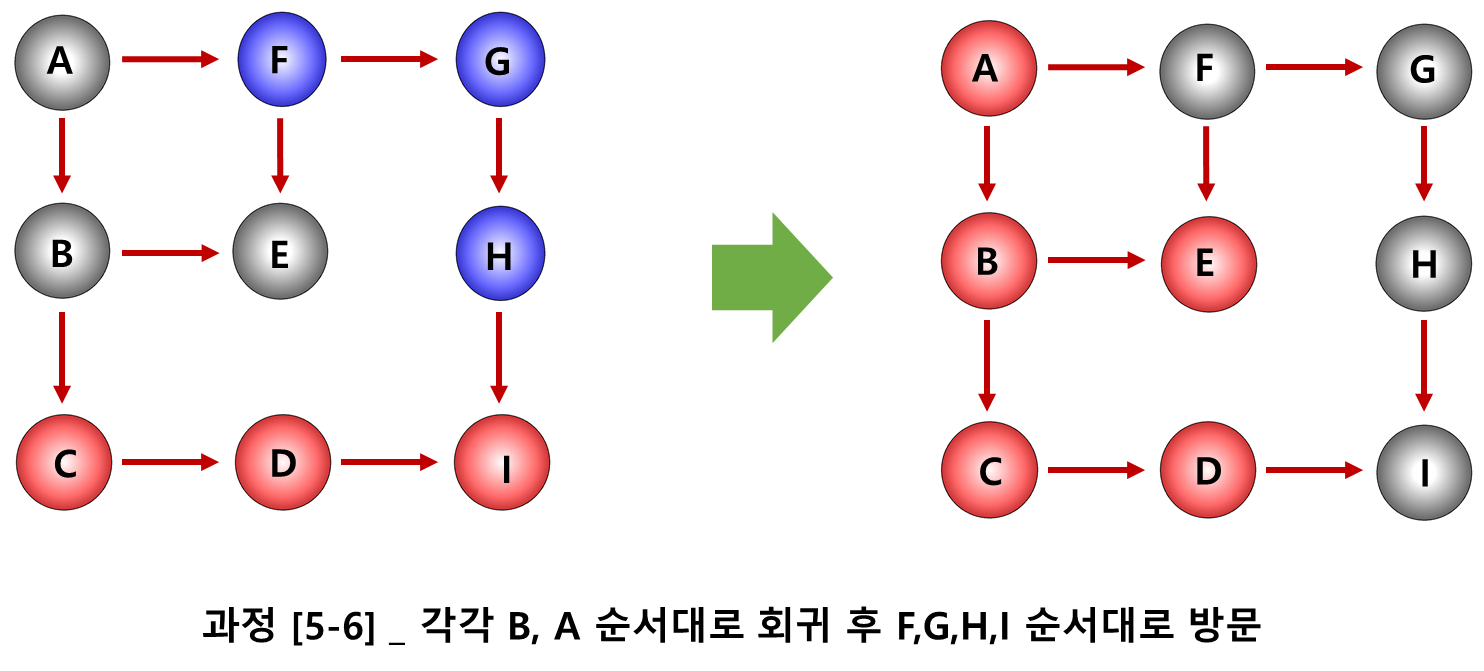
이전의 이진트리 순회 알고리즘을 생각하면, DFS알고리즘도 얼추 감이 올 것이기 때문에 마지막 과정은 생략해두겠다.
2. 알고리즘 구현 _ 깊이 우선 탐색(Depth First Search)
실제로 백트래킹을 구현해보면 위 과정으로 진행하지는 않고 에지 집합의 순서에 따라 다르다. 다만 어떤 느낌인지만 보여주기 위해서 예를 든 것이다. 다음의 예시 코드로 탐색 결과를 확인해보자.
예시 코드:
def DFS(G,v,vlist):
vlist[v]=True
print("Visit : " +v.getv() )
for E in v.getkeys():
if E not in vlist:
DFS(G,E,vlist)
def DFSTravel(G):
vlist={}
for v in G:
DFS(G,v,vlist)
코드 결과:
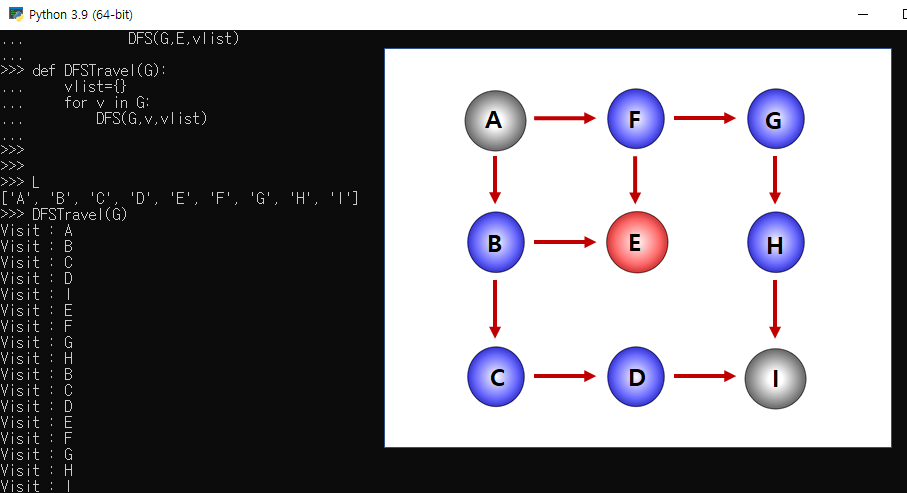
* 위의 방문 결과를 이해하는 것이 곧 DFS의 이해이며, 백트래킹을 완벽히 이해한 것이라고 볼 수 있다.
정리하자면, DFS 알고리즘은 자료를 깊이를 우선하여 각각의 자료를 탐색한다. 이는 트리 형태의 자료구조에서도 동일한 측면을 가지는데, 예를 들어 트리로 구성된 자료에 대한 검색을 시도할 때 DFS 알고리즘을 사용할 수 있다. 트리의 경우, 레벨 탐색이 아닌 전위 순회 알고리즘이 바로 DFS알고리즘이 된다. 그리고 잎 노드에 가까운 자료일수록 DFS 알고리즘은 빠른 탐색 결과를 보여준다.
마지막으로 그래프의 경우에 어떤 방식으로 자료를 구성했는지에 따라 시간 복잡도의 차이를 보이기도 한다. 예를 들어, 인접 리스트 방식으로 그래프를 구현했다면 시간 복잡도는 O(V+E)이다. 반대로 인접 행렬로 구현한 그래프의 시간 복잡도는 O(V2)이다.
* DFS기법의 의의는 모든 벌텍스에 접근하는 방법이라는 측면에서 중요하다. 이는 이후의 다른 알고리즘에서 여러 가지 응용된 형태로 다시 등장할 것이기 때문이다.
'COMPUTER SCIENCE > Algorithmic & Data Structure' 카테고리의 다른 글
| [Section 6] 정렬 알고리즘의 종류와 특징 (0) | 2022.01.18 |
|---|---|
| [Section 8] 알고리즘 설계 기초 _ 분류(Classification) (0) | 2022.01.17 |
| [Section 4] 그래프와 큐의 혼합 _ 방문 상태 체크 (0) | 2022.01.15 |
| [Section 4] 그래프 알고리즘 _ 인접 리스트(Adjacency List) (0) | 2022.01.13 |
| [Section 3] 파이썬 큐 모듈 사용법 _ 복잡도 분석&비교 (0) | 2022.01.12 |



