자료구조와 알고리즘 목차 보기
[INTRO] 자료구조와 알고리즘
자료구조와 알고리즘에 대해서... 자료구조는 프로그래밍에서 사용되는 데이터를 어떻게 표현하는 것인가에 대한 컴퓨터 과학 분야이다. 그리고 알고리즘은 표현된 데이터를 계산하는 방법에
hookspedia.tistory.com
0. INTRO
이전에 언급한 바와 같이 순회 기능은 이진트리의 주 ADT 중 하나이다. 하지만 순회 기능에도 다양한 용어가 사용된다. 따라서 이번에는 이진트리의 순회 기능의 용어와 그 개념에 대해 알아보고 알고리즘을 구현해보고자 한다. 참고로 이진트리의 구현을 위해서는 스택 알고리즘이 선행되어야 한다.
1. 순회(Traversal) 기능을 위한 함수 정리
순회 기능은 트리의 모든 노드로 접근하게 만들어주는 중요한 기능이다. 그리고 순회의 결과로써 데이터를 스택이나 큐 형태로 저장하면, 접근한 데이터의 순서를 알 수 있다. 이진트리에서는 총 6가지 순서로 데이터를 탐색할 수 있는데, 다음의 용어를 보자.
LDR, LRD, DLR, DRL, RDL, RLD
이 순회의 6가지 용어는 순회의 구현 방법에 따라 3가지 종류로 함축되어 나타낼 수도 있다. 예를 들어, 이진 트리에서 DLR, LDR, LRD 이 세 가지 순서는 다음의 탐색 순서를 갖는다.


2. 순회 종류와 함수 구현 _ 전위 순회, 중위 순회, 그리고 후위 순회
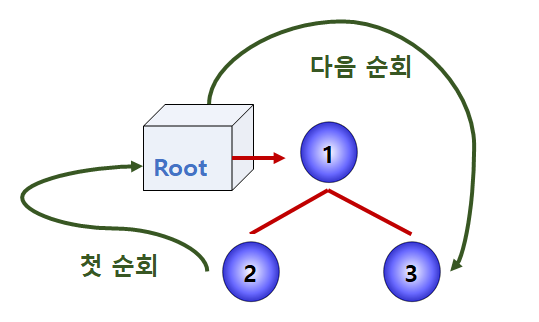
전위 순회(Preorder Traversal) 기능은 루트 노드를 가장 먼저 접근하는 방식의 순회 기능이다.
이 전위 순회 기능은 위에서 정리된 DLR 기능에 해당하는데, 현재 노드를 가장 먼저 방문한다는 의미이다.
전위 순회 기능은 보통 재귀 함수로 간단히 구현 할 수 있다.
전위 순회 함수:
def Preorder(root,result):
if not root:
return
result.append(root.data)
Preorder(root.Lchild,result)
Preorder(root.Rchild,result)
예를 들어, 다음과 같은 왼쪽 그림의 트리가 존재한다고 가정하면 트리의 순회과정은 오른쪽과 같다.


따라서 전위 순회 함수의 결과는 1,2,3 이 된다. (스택은 그냥 리스트로 구현하였다.)
중위 순회(Inorder Traversal) 기능은 왼쪽의 하위 트리에 먼저 접근하는 방식이다.
이 기능은 앞서 정의한 LDR에 해당한다고 할 수 있겠다.
마찬가지로 중위 순회 또한 다음과 같이 재귀 함수로 구현해두겠다.
중위 순회 함수:
def Inorder(root,result):
if not root:
return
Inorder(root.Lchild,result)
result.append(root.data)
Inorder(root.Rchild,result)
같은 트리 예시로 순회 과정을 보면 다음과 같다.


따라서 전위 순회 함수의 결과는 2,1,3 이 된다.
마지막으로 후위 순회(Postorder Traversal) 기능은 오른쪽의 하위 트리에 먼저 접근하는 방식이다.
이 기능은 앞서 정의한 LRD에 해당한다고 할 수 있겠다.
마찬가지로 후위 순회 또한 다음과 같이 재귀 함수로 구현해두겠다.
후위 순회 함수:
def Postorder(root,result):
if not root:
return
Postorder(root.Lchild,result)
Postorder(root.Rchild,result)
result.append(root.data)
같은 트리 예시로 순회 과정을 보면 다음과 같다.


따라서 후위 순회 함수의 결과는 2,3,1 이 된다.
* 반복문으로도 구현이 가능하나, 시간 복잡도와 공간 복잡도 측면은 모두 O(n)으로 동일하기 때문에 따로 구현은 하지 않겠다. 하지만 재귀 함수의 단점을 명시하고는 있어야 한다.
위에서 예시로 아주 간단한 트리에 대해서 알아보았다. 그런데 만약 트리가 하나의 층이 더 존재했다면 순회 과정은 어떻게 되었을까? 위에서 구현한 함수는 재귀 함수이기 때문에 재귀적으로 사고해야 결과를 머릿속에서 그려낼 수 있다. 다음의 예시를 보자.

먼저 전위 순회 결과 스택에는 [1,2,4,5,3,6,7] 리스트가 생성된다.
그리고 중위 순회 결과 스택에는 [4, 2, 5, 1, 6, 3, 7] 리스트가 생성된다.
마지막으로 후위 순회 결과 스택에는 [4, 5, 2, 6, 7, 3, 1] 리스트가 생성된다.
그렇다면 레벨 순서인 [1, 2, 3, 4, 5, 6, 7]로 순회하는 것도 가능할까?
3. 레벨 순회 알고리즘 _ 큐와 혼합하기
큐와 이진트리를 혼합하면, 레벨 순서로도 탐색이 가능하다. 다음의 예시 코드를 참고하자.
예시 코드:
from queue import Queue
def levelQ(root):
if not root:
return
Q=Queue()
Q.put(root)
result=[]
node=None
while not Q.empty():
node=Q.get()
result.append(node.getD())
if node.getLchild() !=None:
Q.put(node.getLchild())
if node.getRchild() !=None:
Q.put(node.getRchild())
return result
코드 결과:

'COMPUTER SCIENCE > Algorithmic & Data Structure' 카테고리의 다른 글
| [Section 4] 그래프 알고리즘 _ 인접 행렬(Adjacency matrix) (0) | 2022.01.11 |
|---|---|
| [Section 4] 그래프 구현 알고리즘의 종류 (0) | 2022.01.11 |
| [Section 3] 스택 알고리즘 _ 배열 스택(Array Stack) (0) | 2022.01.11 |
| [Section 4] 노드 알고리즘 구현 _ 이진 트리(Binary Trees) (0) | 2022.01.11 |
| [Section 5] 힙(Heap)의 개념과 용어 정리 (0) | 2022.01.10 |



