자료구조와 알고리즘 목차 보기
[INTRO] 자료구조와 알고리즘
자료구조와 알고리즘에 대해서... 자료구조는 프로그래밍에서 사용되는 데이터를 어떻게 표현하는 것인가에 대한 컴퓨터 과학 분야이다. 그리고 알고리즘은 표현된 데이터를 계산하는 방법에
hookspedia.tistory.com
0. INTRO
비-선형 자료구조는 자료가 순차적이지 않는 자료구조를 의미한다. 비-선형 자료구조는 대표적으로 트리와 그래프가 존재하는데, 이번에는 그래프 자료구조의 개념을 이해해보도록 하자.
1. 비-선형 자료구조 _ 그래프의 개념
트리 구조는 룻트가 가리키는 데이터의 출발이 시작이라면, 그래프 구조는 룻트가 없는 트리와 비슷한 구조를 갖는다. 물론 각 데이터들은 자료의 형태에 따라 포인터가 가리키는 노드가 달라진다. 다음과 데이터 구조 그림을 참고해보자.

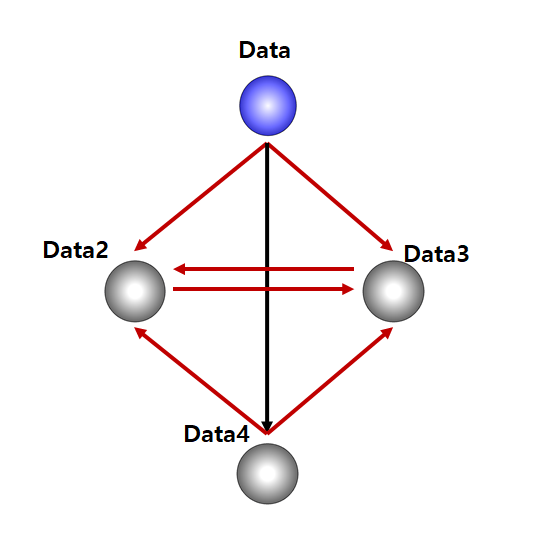
위의 그림에서 보인 것처럼 그래프 구조는 어떻게 노드를 구성하고 각 데이터를 연결하느냐에 따라 데이터 구조가 확연히 달라진다. 다시 말해서, 시작을 가리키는 포인터가 없기 때문에 데이터 선택에 자유를 가지고 어떤 데이터의 접근 가능 여부가 시작 데이터의 선택에 달려있다는 것이다.
그래프 구조에 더 친숙해 지기 위해서 그래프 용어에 대해 알아보도록 하자.
2. 그래프의 표현 방법 _ 꼭짓점 노드(Vertex) 와 간선(Edge)
이전 그래프의 기본 개념에서 꼭짓점 노드와 간선을 통해서 그래프가 어떤 방식으로 구성되었는지 알아보았다. 이번에는 알고리즘을 구현하기 전에 그래프의 표현 방식에 익숙해지도록 하자. 어떤 그래프의 표현을 위해 통상적으로 그래프는 다음과 같이 꼭짓점 노드 V와 간선 E를 쌍으로 나타낸다.
(V, E)
여기에서 V는 그래프를 구성하는 노드의 집합을 의미하고, 간선 E는 꼭짓점 노드의 연결 상태를 지칭하는 원소들의 집합으로 정의된다. 이렇게 두 개로 분류된 데이터 쌍(piar)은 방향 간선(Directed edge) 혹은 비-방향 간선 (Undirected edge)라 불리는 관계를 가지고 있다. 그 의미는 다음의 그림을 참고하자.

방향 간선와 비-방향 간선의 차이는 무엇인가? 바로 쌍의 관계가 단 방향이냐, 양 방향이냐에 있다. 예를 들어 임의의 꼭짓점 노드 V1과 V2의 연결상태를 지칭하는 간선 E가 방향 간선 이라고 가정하자. 방향이 어디로 향하느냐에 따라 벌텍스의 접근 경로가 정해진다. 반대로, 비-방향 간선의 경우에 어떤 꼭짓점 노드에서든지간에 서로에게 접근이 가능하다. 따라서 비-방향 간선은 노드 쌍의 관계가 양 방향인 것이다.
정리하자면 다음과 같다.
- 방향 간선(Directed edge)이라 함은 어떤 간선원소 쌍에 해당하는 노드들은 단 방향으로만 접근이 가능하다는 것을 의미한다.
- 비 방향 간선(Undirected edge)이라 함은 어떤 간선 원소 쌍에 해당하는 노드들은 양 방향으로 서로 접근이 가능함을 의미한다.
3. 그래프 용어 정리
앞서 정리한 그래프의 표현을 바탕으로 다음과 같이 그래프 용어를 정리하자.
- 방향 그래프(Directed Graph)와 비 방향 그래프(Undirected Graph)는 그래프의 노드 상태를 지칭하는 용어이다. 예를 들어, 방향 그래프는 모든 간선들이 단 방향임을 의미하고, 비 방향 그래프는 모든 간선들이 양 방향임을 의미한다. 다음의 그림을 참고하자.

- 셀프 고리(self loop)란 벌텍스가 자기 자신과 연결된 상태를 지칭한다. 이것을 순환(cyclic) 특성이라고 하는데, 만약 그래프가 비순환(acyclic) 특성을 가지면 트리(tree)가 된다. 예를 들어, 다음의 트리와 그래프는 동일한 자료 구성을 가진다.

* 간선을 통해서 자기 자신을 마주하게 되는 경우 또한 순환이라고 한다.
- 두 간선이 평행하다는 말은 다음의 그림과 같은 의미이다.

- 두 꼭짓점 노드가 서로 인접해있다는 의미는 두 꼭짓점 노드가 어떤 방식으로든 연결되어있다는 말과 같다. 추가로 꼭짓점 노드의 정도(Degree of a vertex)는 어떤 꼭짓점 노드와 연결된 간선의 수를 일컫는다.
- 하위 그래프는 그래프의 엣지를 기준으로 하는 하위 집합을 의미한다. 물론 간선과 만나는 꼭짓점 노드 또한 포함한다.
- 어떤 꼭짓점 노드로부터 다른 꼭짓점 노드까지 연결된 일련의 간선들을 경로(path)라고 한다. 단순 경로(simple path)는 경로상에서 동일한 꼭짓점 노드의 중복을 허용하지 않는 경로이다.
- 그래프끼리도 연결이 가능한데 이 경우, 모든 꼭짓점 노드가 다른 그래프까지 접근할 수 있는 경로가 반드시 하나는 존재해야 한다. 이 말은 연결되지 않는 그래프는 연결된 원소 집합으로 구분이 가능하다는 말과 동일하다.
- 그래프에서 방향 비순환 그래프(Directed acylic graph)라는 용어를 사용한다. 이는 DAG라고 부르는데, 순환 특성이 존재하지 않는 방향 그래프를 의미한다. 따라서 DAG는 트리가 될 수 있는 그래프이다.
- 어떤 그래프의 모든 꼭짓점 노드가 다른 모든 꼭짓점 노드를 연결하는 간선을 가지면, 완전 그래프(Complete Graph)라고 부른다.
- 가중치 그래프(Weighted Graph)는 정수 형태의 가중치(weights)를 나타낸 그래프이다. 이때 가중치는 경로의 거리를 나타 낼 수도 있으며 정수 형태의 어떤 비용을 임의로 간선 원소에 할당 할 수도 있다. 예를 들어, 가중치가 경로의 거리를 나타낸다면, 다음의 그림과 같이 그래프를 도식화할 수 있다.

* 따라서 가중치 그래프는 어떤 그래프의 하위 그래프이기도 하다.
'COMPUTER SCIENCE > Algorithmic & Data Structure' 카테고리의 다른 글
| [Section 5] 힙(Heap)의 개념과 용어 정리 (0) | 2022.01.10 |
|---|---|
| [Section 5] 우선 순위 큐의 개념과 종류 &시간 복잡도 (0) | 2022.01.10 |
| [Section 4] 트리(Tree)의 개념 이해 _ 트리 용어 정리 (0) | 2022.01.10 |
| [Section 3] 큐(Queue)의 종류와 개념 이해하기 (0) | 2022.01.07 |
| [Section 3] 스택(Stack)의 종류와 개념 이해하기 (0) | 2022.01.07 |


